题目内容
判断下列方程的解法是否正确,如若不对,请改正.
解方程
x2+x=2.
解:原方程可化为2x2+3x-6=0,
这里a=2,b=3,c=-6.
则b2-4ac=32-4×2×(-6)=9+48=57,
所以x=
,x1=
x2=
.
解方程
| 2 |
| 3 |
解:原方程可化为2x2+3x-6=0,
这里a=2,b=3,c=-6.
则b2-4ac=32-4×2×(-6)=9+48=57,
所以x=
-3±
| ||
| 2 |
-3+
| ||
| 2 |
-3-
| ||
| 2 |
分析:先化为整系数方程,然后利用公式法求解.
解答:解:原方程可化为2x2+3x-6=0,
a=2,b=3,c=-6.
b2-4ac=32-4×2×(-6)=9+48=57,
x=
,
所以x1=
x2=
.
此解法正确.
a=2,b=3,c=-6.
b2-4ac=32-4×2×(-6)=9+48=57,
x=
-3±
| ||
| 2 |
所以x1=
-3+
| ||
| 2 |
-3-
| ||
| 2 |
此解法正确.
点评:本题考查了解一元二次方程:把x=
(b2-4ac≥0)叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式;用求根公式解一元二次方程的方法是公式法.
-b±
| ||
| 2a |

练习册系列答案
相关题目



 ,
,
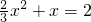 .
. ,x1=
,x1=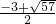 x2=
x2=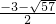 .
. 。
。