Question

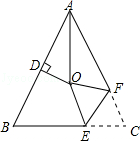
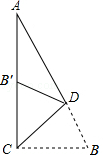
如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于【   】

A．25°

B．30°

C．35°

D．40°

Answer 1

D。

∵在Rt△ACB中，∠ACB=90°，∠A=25°，∴∠B=90°﹣25°=65°。
∵△CDB′由△CDB反折而成，∴∠CB′D=∠B=65°。
∵∠CB′D是△AB′D的外角，∴∠ADB′=∠CB′D﹣∠A=65°﹣25°=40°。
故选D。