题目内容
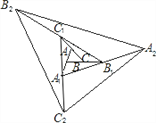
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )
A. 6 B. 5 C. 4 D. 3
【答案】C
【解析】试题分析:先根据已知条件求出△A1B1C1及△A2B2C2的面积,再根据两三角形的倍数关系求解即可.
解:△ABC与△A1BB1底相等(AB=A1B),高为1:2(BB1=2BC),故面积比为1:2,
∵△ABC面积为1,
∴S△A1B1B=2.
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可证△A2B2C2的面积=7×△A1B1C1的面积=49,
第三次操作后的面积为7×49=343,
第四次操作后的面积为7×343=2401.
故按此规律,要使得到的三角形的面积超过2015,最少经过4次操作.
故选C.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目