题目内容
下列命题中( )
①三边对应平行的两个三角形全等
②有一边对应相等,其余两边对应平行的两个三角形全等
③有一边重合,其余两边对应平行的两个三角形全等.
①三边对应平行的两个三角形全等
②有一边对应相等,其余两边对应平行的两个三角形全等
③有一边重合,其余两边对应平行的两个三角形全等.
分析:根据已知画出反例图形,即可判断①②,画出图形,根据平行线的性质得出两角对应相等,再根据全等三角形的判定即可得出两个三角形全等,即可判断③.
解答:解:∵如图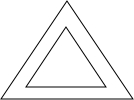
两三角形的三边互相平行,但是两三角形不全等,∴①错误;
∵如图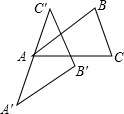
AC=A′C′,AB∥A′B′,BC∥B′C′,但两三角形不全等,∴②错误;
∵如图,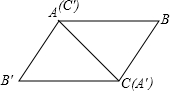
根据平行线的性质得出∠BAC=∠B′C′A′,∠BCA=∠B′A′C′,根据ASA推出△ABC≌△C′A′B′,∴③正确;
故选C.

两三角形的三边互相平行,但是两三角形不全等,∴①错误;
∵如图

AC=A′C′,AB∥A′B′,BC∥B′C′,但两三角形不全等,∴②错误;
∵如图,

根据平行线的性质得出∠BAC=∠B′C′A′,∠BCA=∠B′A′C′,根据ASA推出△ABC≌△C′A′B′,∴③正确;
故选C.
点评:本题考查了全等三角形的判定和平行线的性质的应用,注意:全等三角形的判定定理是:SAS,ASA,AAS,SSS.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目