题目内容
已知m是质数,x、y均为整数,则方程|x+y|+
=m的解的个数是( )
| x-y |
| A、2 | B、4 | C、5 | D、无数个 |
分析:首先由x+y与x-y的奇偶性相同,可得m是偶数,又由m是质数,可得m=2,则可分析求解,得到答案.
解答:解:∵x+y与x-y的奇偶性相同,而
也只能是整数,
∴m是偶数,
∵m是质数,
∴m=2,
于是有
,
,
,
,
,
以上5个方程组均有整数解.
故选C.
| x-y |
∴m是偶数,
∵m是质数,
∴m=2,
于是有
|
|
|
|
|
以上5个方程组均有整数解.
故选C.
点评:此题考查了质数的意义,整数奇偶性问题的知识.题目难度适中,注意别漏解.

练习册系列答案
相关题目
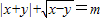 的解的个数是( )
的解的个数是( )