题目内容
 如图,已知点M是以AB为直径的半圆上的一个三等分点,点N是弧BM的中点,点P是直径AB上的点.若⊙O的半径为1.
如图,已知点M是以AB为直径的半圆上的一个三等分点,点N是弧BM的中点,点P是直径AB上的点.若⊙O的半径为1.(1)用尺规在图中作出点P,使MP+NP的值最小(保留作图痕迹,不写作法);
(2)求MP+NP的最小值.
分析:(1)作点M关于直线AB的对称点M′,连接M′N交直径AB于点P,则点P即为所求点,M′N的长即为MP+NP的最小值;
(2)连接OM′,ON,先判断出△OM′N的形状,再根据勾股定理求解即可.
(2)连接OM′,ON,先判断出△OM′N的形状,再根据勾股定理求解即可.
解答:解:(1)如图1所示;
(2)如图2, 连接OM′,ON,
连接OM′,ON,
∵点M是以AB为直径的半圆上的一个三等分点,点N是弧BM的中点,
∴∠BON=360°×
=30°,
∠M′OB=360°×
=60°,
∴∠M′ON=90°,
∴△OM′N是等腰直角三角形,
∴M′N=
=
=
.
(2)如图2,
 连接OM′,ON,
连接OM′,ON,∵点M是以AB为直径的半圆上的一个三等分点,点N是弧BM的中点,
∴∠BON=360°×
| 1 |
| 12 |
∠M′OB=360°×
| 1 |
| 6 |
∴∠M′ON=90°,
∴△OM′N是等腰直角三角形,
∴M′N=
| ON2+OM′2 |
| 12+12 |
| 2 |
点评:本题考查的是轴对称-最短路线问题,熟知两点之间,线段最短是解答此题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
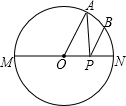 如图,已知点A是以MN为直径的半圆上一个三等分点,点B是AN的中点,点P是半径ON上的点,若⊙O的半径为1,则AP+BP的最小值为
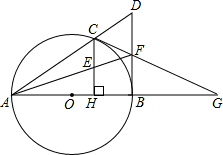
如图,已知点A是以MN为直径的半圆上一个三等分点,点B是AN的中点,点P是半径ON上的点,若⊙O的半径为1,则AP+BP的最小值为 (2012•德阳)如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(2012•德阳)如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.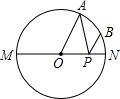 如图,已知点A是以MN为直径的半圆上一个三等分点,点B是
如图,已知点A是以MN为直径的半圆上一个三等分点,点B是