题目内容
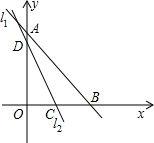 如图,直线l1过A(0,2),B(2,0)两点,直线l2:y=mx+b过点(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.
如图,直线l1过A(0,2),B(2,0)两点,直线l2:y=mx+b过点(1,0),且把△AOB分成两部分,其中靠近原点的那部分是一个三角形,设此三角形的面积为S,求S关于m的函数解析式,及自变量m的取值范围.
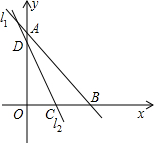 解:∵直线L1过点A(0,2),B(2,0),直线L2:y=mx+b过点C(1,0)且
解:∵直线L1过点A(0,2),B(2,0),直线L2:y=mx+b过点C(1,0)且把△AOB分成两部分中靠近原点的那部分是一个三角形,
∴可以推出直线L2过第一、二、四象限,
所以可以设直线L2交y轴与D点(0,b),
∵围成的三角形面积为S,根据三角形面积公式可得,
S=
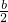 ,
,则b=2S 也即D点坐标为(0,2S),
将C、D点坐标代入直线L2的解析式,可解出,
m=-2S,
∴S关于m的函数解析式为:S=-
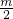 ,
,∵S>0且S小于△AOB面积的一半,所以0<S≤1,
∴0<-
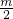 ≤1,
≤1,∴-2≤m<0
∴自变量m的取值范围是:-2≤m<0.
分析:根据已知首先表示出围成的三角形面积为S,得出b=2S 即D点坐标为(0,2S),再将C、D点坐标代入直线L2的解析式,可解出即可.
点评:此题主要考查了一次函数的综合应用,根据已知得出D点坐标,从而利用图象上点的坐标性质得出是解决问题的关键.

练习册系列答案
相关题目
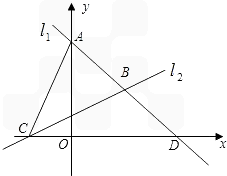
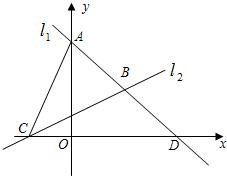 点C,两直线l1,l2相交于点B.
点C,两直线l1,l2相交于点B.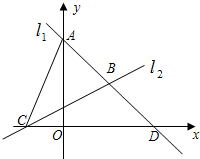 如图,直线l1过点A(0,4),点D(4,0),直线l2:
如图,直线l1过点A(0,4),点D(4,0),直线l2: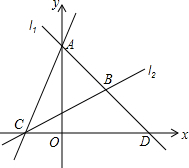 如图,直线l1过点A(0,4)、D(4,0)两点,直线l2:y=
如图,直线l1过点A(0,4)、D(4,0)两点,直线l2:y=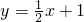 与x轴交于
与x轴交于 点C,两直线l1,l2相交于点B.
点C,两直线l1,l2相交于点B.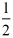 x+1与x轴交于点C,两直线l1,l2相交于点B.
x+1与x轴交于点C,两直线l1,l2相交于点B.