题目内容
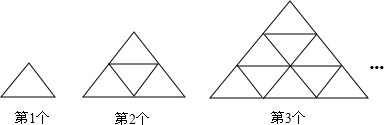
下列图案是由斜边相等的等腰直角三角形按照一定的规律拼接而成的.依此规律,第9个图案中的三角形与第一个图案中的三角形能够全等的共有___个.

- A.49
- B.64
- C.81
- D.100
C
分析:根据图形找出规律,即第几个就有几的平方个小三角形,所以第9个图案中的全等小等腰直角三角形的个数就是92个,即81个,可推出结论.
解答:第2个中有4个全等的小等腰直角三角形,即有22个全等的小等腰直角三角形,
第3个中有9个全等的小等腰直角三角形,即有32个全等的小等腰直角三角形,
则第9个中应有92个全等的小等腰直角三角形,
所以第9个图案中的全等的小等腰直角三角形的个数为81个.
故选C.
点评:本题考查了规律型:图形的变化.解题的关键是找到每个图形中小三角形的个数与图形的序号之间的关系.
分析:根据图形找出规律,即第几个就有几的平方个小三角形,所以第9个图案中的全等小等腰直角三角形的个数就是92个,即81个,可推出结论.
解答:第2个中有4个全等的小等腰直角三角形,即有22个全等的小等腰直角三角形,
第3个中有9个全等的小等腰直角三角形,即有32个全等的小等腰直角三角形,
则第9个中应有92个全等的小等腰直角三角形,
所以第9个图案中的全等的小等腰直角三角形的个数为81个.
故选C.
点评:本题考查了规律型:图形的变化.解题的关键是找到每个图形中小三角形的个数与图形的序号之间的关系.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 9、下列图案是由斜边相等的等腰直角三角形按照一定的规律拼接而成的.依此规律,第9个图案中的三角形与第一个图案中的三角形能够全等的共有( )个.
9、下列图案是由斜边相等的等腰直角三角形按照一定的规律拼接而成的.依此规律,第9个图案中的三角形与第一个图案中的三角形能够全等的共有( )个.