题目内容
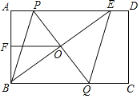
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD,BE,BC于点P,O,Q,连接BP,EQ.
(1)求证:四边形BPEQ是菱形;
(2)F为AB的中点,则线段OF与线段AE有什么位置关系和数量关系,并说明理由;
(3)在(2)的条件下,若AB=6,OF=4,求PQ的长.
【答案】(1)见解析;(2)见解析;(3)PQ=![]() .
.
【解析】
(1)先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形BPEQ是平行四边形,再根据菱形的判定即可得出结论;
(2)根据中位线定理即可求出线段OF与线段AE的位置关系和数量关系.
(3)根据勾股定理求出OB的长度,进而求出BE, 设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,根据勾股定理列出方程,求出边长,根据菱形的面积公式进行求解即可.
(1)证明:∵PQ垂直平分BE,
∴PB=PE,OB=OE,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PEO=∠QBO,
在△BOQ与△EOP中,∠PEO=∠QBO,OB=OE,∠POE=∠QOB,
∴△BOQ≌△EOP(ASA),
∴PE=QB,
又∵AD∥BC,
∴四边形BPEQ是平行四边形,
又∵QB=QE,
∴四边形BPEQ是菱形;
(2)∵四边形BPEQ是菱形,
∴OB=OE.
又∵F是AB的中点,
∴OF是△BAE的中位线,
∴AE∥OF且OF=![]() AE.
AE.
(3)∵AB=6,F是AB的中点,
∴BF=3.
∵OF∥AE,
∴∠BFO=90°.
在Rt△FOB中, ![]()
∴BE=10.
设菱形的边长为x,则AP=8﹣x.
在Rt△APB中,BP2=AB2+AP2,即x2=62+(8﹣x)2,解得:x=![]() .
.
由菱形的面积公式可知: ![]() 解得:PQ
解得:PQ![]()

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目