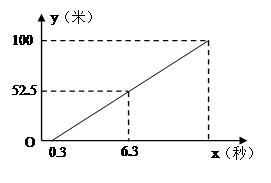题目内容
为弘扬体育精神,锻炼师生体魄,我校组织了今年春季运动会.在男子100米预赛中,高二年级某同学甲在发令枪响的同时立即起跑,起跑后甲与起点的距离与甲起跑后的时间大致满足正比例函数的关系.如果用y(米)表示与起点的距离,用x(秒)表示起跑后的时间,测得两个瞬间的x、y如下表:
|
起跑后的时间x(秒) |
3 |
9 |
|
与起跑点距离y(米) |
24 |
72 |
(1)求同学甲跑动过程中的函数关系式,并写出x的取值范围?
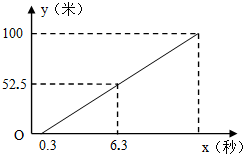
(2)如果同组另一位同学乙在发令枪响后与起点的距离与发令枪响后的时间大致满足下面的图像,请问:同学乙能否超越同学甲?若能,请通过计算求出在何时超越?

【答案】
(1)甲同学的函数为 (0≤x≤12.5)(2)甲起跑7.5秒后,乙同学可以超越甲
(0≤x≤12.5)(2)甲起跑7.5秒后,乙同学可以超越甲
【解析】解:(1)甲同学的函数为 (0≤x≤12.5)
(0≤x≤12.5)
(2)乙同学的函数为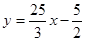 (0≤x≤12.3)
(0≤x≤12.3)
甲、乙与起跑点距离相等时,列方程: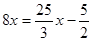
解 得:x=7.5
答:在甲起跑7.5秒后,乙同学可以超越甲;
(或:在乙起跑7.2秒后,乙同学可以超越甲.)
(1)把(3,24),(9,72)代入y=kx,求得函数关系式
(2)通过图像求出乙同学的函数关系式,列方程求解
|

练习册系列答案
相关题目
 为弘扬体育精神,锻炼师生体魄,我校组织了今年春季运动会.在男子100米预赛中,高二年级某同学甲在发令枪响的同时立即起跑,起跑后甲与起点的距离与甲起跑后的时间大致满足正比例函数的关系.如果用y(米)表示与起点的距离,用x(秒)表示起跑后的时间,测得两个瞬间的x、y如下表:
为弘扬体育精神,锻炼师生体魄,我校组织了今年春季运动会.在男子100米预赛中,高二年级某同学甲在发令枪响的同时立即起跑,起跑后甲与起点的距离与甲起跑后的时间大致满足正比例函数的关系.如果用y(米)表示与起点的距离,用x(秒)表示起跑后的时间,测得两个瞬间的x、y如下表:
| 起跑后的时间x(秒) | 3 | 9 |
| 与起跑点距离y(米) | 24 | 72 |
(2)如果同组另一位同学乙在发令枪响后与起点的距离与发令枪响后的时间大致满足下面的图象,请问:同学乙能否超越同学甲?若能,请通过计算求出在何时超越?
为弘扬体育精神,锻炼师生体魄,我校组织了今年春季运动会.在男子100米预赛中,高二年级某同学甲在发令枪响的同时立即起跑,起跑后甲与起点的距离与甲起跑后的时间大致满足正比例函数的关系.如果用y(米)表示与起点的距离,用x(秒)表示起跑后的时间,测得两个瞬间的x、y如下表:
| 起跑后的时间x(秒) | 3 | 9 |
| 与起跑点距离y(米) | 24 | 72 |
(2)如果同组另一位同学乙在发令枪响后与起点的距离与发令枪响后的时间大致满足下面的图像,请问:同学乙能否超越同学甲?若能,请通过计算求出在何时超越?