题目内容
学习了整式的加减运算后,老师给同学们布置了一道课堂练习题“a=-2,b=2010时,求(3a2b-2ab2+4a)-2(2a2b-3a)+2(ab2+| 1 | 2 |
亲爱的同学们,你相信盈盈的说法吗?说说你的理由.
分析:首先化简代数式,通过去括号、合并同类项,得出结论即含有b的代数式相加为0,即可说明.
解答:解:原式=3a2b-2ab2+4a-4a2b+6a+2ab2+a2b-1
=10a-1,
当a=-2时,原式=10×(-2)-1=-21.
因为化简后的结果中不再含有字母b,故最后的结果与b的取值无关,因此说b=2010这个条件是多余的.
所以盈盈的说法是正确的.
=10a-1,
当a=-2时,原式=10×(-2)-1=-21.
因为化简后的结果中不再含有字母b,故最后的结果与b的取值无关,因此说b=2010这个条件是多余的.
所以盈盈的说法是正确的.
点评:此题考查的知识点是整式的加减-化简求值,关键是正确进行整式的加减运算说明道理.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
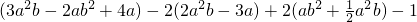 的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.
的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话. 的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.亲爱的同学们,你相信盈盈的说法吗?说说你的理由.
的值”.盈盈做完后对同桌说:“张老师给的条件b=2010是多余的,这道题不给b的值,照样可以求出结果来.”同桌不相信她的话.亲爱的同学们,你相信盈盈的说法吗?说说你的理由.