题目内容
【题目】如图1,A1B1和A2B2是水面上相邻的两条赛道(看成两条互相平行的线段).甲是一名游泳运动健将,乙是一名游泳爱好者,甲在赛道A1B1上从A1处出发,到达B1后,以同样的速度返回A1处,然后重复上述过程;乙在赛道A2B2上以2m/s的速度从B2处出发,到达A2后以相同的速度回到B2处,然后重复上述过程(不考虑每次折返时的减速和转向时间).若甲、乙两人同时出发,设离开池边B1B2的距离为y(m),运动时间为t(s),甲游动时,y(m)与t(s)的函数图象如图2所示.

(1)赛道的长度是 m,甲的速度是 m/s;
(2)分别写出甲在0≤t≤20和20<t≤40时,y关于t的函数关系式:当0≤t≤20,y= ; 当20<t≤40时,y= ;
(3)在图2中画出乙在2分钟内的函数大致图象(用虚线画);
(4)请你根据(3)中所画的图象直接判断,若从甲、乙两人同时开始出发到2分钟为止,甲、乙共相遇了几次?2分钟时,乙距池边B1B2的距离为多少米。
【答案】(1) 50,2.5;(2) y=-2.5t+50,y=3t-60.(3)画图见解析;(4)5,20.
【解析】
试题分析:(1)由函数图象可以直接得出赛道的长度为50米,由路程÷时间=速度就可以求出甲的速度.
(2)先根据图象的形状,可判断出甲在0≤t≤20和20<t≤40时,y都是t的一次函数,设出其解析式,再运用待定系数法求解;
(3)乙的速度为2m/s,由B2到达A2的路程为赛道的长度50m,根据时间=路程÷速度,即可求出乙船由B2到达A2的时间为25s;乙船在2分钟内可运动2个来回,每25s可从赛道一端运动到另外一端,起点在原点,据此在图2中画出乙船在2分钟内的函数图象;
(4)两个图象的交点个数即为相遇次数,根据乙船在2分钟内可运动2个来回,每25s可从赛道一端运动到另外一端,所以2分钟时,乙距池边B1B2的距离为20秒所游的路程.
试题解析:(1)由图象,得
赛道的长度是:50米,
甲的速度是:50÷20=2.5m/s.
(2)当0≤t≤20时,设y=k1x+b1,
把(0,50),(20,0)代入得:
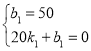 ,
,
解得: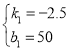
∴y=-2.5t+50,
当20<t≤40时,设y=k2x+b2,
把(20,0),(40,60)代入得:
 ,
,
解得: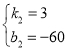
∴y=3t-60.
故答案为:
(3)因为赛道的长度为50米,乙的速度为2米/秒,所以乙船由B2到达A2的时间为25秒;乙在2分钟内的函数图象如图5所示:
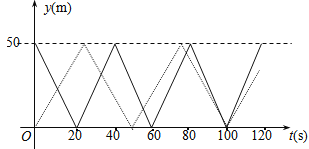
(4)从上图可知甲、乙共相遇5次.
2分钟=120秒,120-25×4=20(s),
∴2分钟时,乙距池边B1B2的距离为:20×2=40(米).


