题目内容
 已知直线l1:
已知直线l1: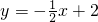 与直线l2:y=2x-3相交于点A.
与直线l2:y=2x-3相交于点A.
(1)求点A坐标;
(2)设l1交y轴子点B,l2交y轴于点C,求△ABC的面积;
(3)若点D与点A、B、C能构成平行四边形,请直接写出D点坐标.
解:(1)由题意得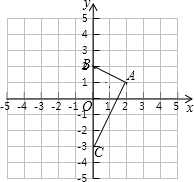

解得: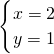
∴A(2,1)
(2)当x=0时,y=2
∴B(0,2)
当x=0时,y=-3
C(0,-3
∴S△ABC=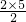
=5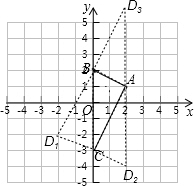
(3)D(-2,-2)、(2,-4)或(2,6)
分析:(1)利用两条直线的解析式建立二元一次方程组,方程组的解就是点A的坐标.
(2)分别求出点B、C的坐标,知道三点坐标就可以求出三角形的面积.
(3)利用平行四边形的性质和判定就可以确定D点的位置,而确定D点的坐标.
点评:本题是一道一次函数综合试题,考查了直线的解析式与二元一次方程的关系,利用点的坐标求三角形的面积,平行四边形的性质和判定的运用.


解得:
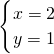
∴A(2,1)
(2)当x=0时,y=2
∴B(0,2)
当x=0时,y=-3
C(0,-3
∴S△ABC=
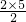
=5

(3)D(-2,-2)、(2,-4)或(2,6)
分析:(1)利用两条直线的解析式建立二元一次方程组,方程组的解就是点A的坐标.
(2)分别求出点B、C的坐标,知道三点坐标就可以求出三角形的面积.
(3)利用平行四边形的性质和判定就可以确定D点的位置,而确定D点的坐标.
点评:本题是一道一次函数综合试题,考查了直线的解析式与二元一次方程的关系,利用点的坐标求三角形的面积,平行四边形的性质和判定的运用.

练习册系列答案
相关题目
 与直线 l2:y=﹣2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=﹣2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .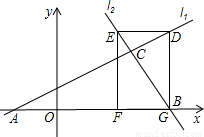
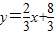 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .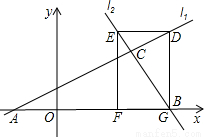
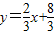 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .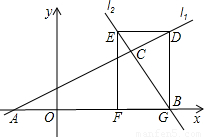
 与直线l2:
与直线l2: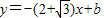 相交于点B(
相交于点B(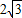 ,2),且直线l2与x轴相交于点A.
,2),且直线l2与x轴相交于点A.