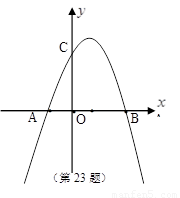题目内容
如图,已知抛物线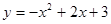 与
与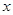 轴的两个交点为A、B,与
轴的两个交点为A、B,与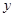 轴交于点C
轴交于点C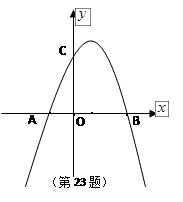
(1)求A、B、C三点的坐标?
(2)用配方法求该二次函数的对称轴和顶点坐标?
(3)若坐标平面内的点M,使得以点M和三点A、B、C为顶点的四边形是平行四边形,求点M的坐标?(直接写出M的坐标,不用说明)
(1)A(-1,0) B(3,0) C(0,3)
(2) ,对称轴
,对称轴 ,顶点(1,4)
,顶点(1,4)
(3)(-5,3)或(4,3)或(2,-3)
解析(1)求与x轴的两个交点,即y=0,求与y轴交于点,即x=0
(2)运用配方法可以求出,注意提取二项系数,各项都要提取,
(3)利用平四边形的性质可以求出
(1)解:y=-x2+2x+3与x轴的两个交点为A、B,
0=-x2+2x+3,
解得:x1=-1,x2=3,
∴A(-1,0)B(3,0),
∵与y轴交于点C,
∴C(0,3);
(2)y=-x2+2x+3,
=-(x2-2x-3),
=-[(x2-2x+1)-4],
=-(x-1)2+4,
对称轴x=1,顶点(1,4);
(3)(-5,3)或(4,3)或(2,-3).

练习册系列答案
相关题目
 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点 .
.
 的坐标;
的坐标; 交
交 .在线段
.在线段 的垂直平分线上是否存在点
的垂直平分线上是否存在点 ,使得点
,使得点 的距离?如果存在,求出点
的距离?如果存在,求出点 作
作 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?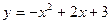 与
与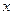 轴的两个交点为A、B,与
轴的两个交点为A、B,与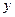 轴交于点C
轴交于点C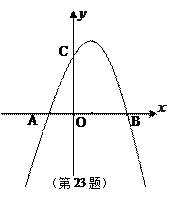
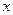 轴交于点
轴交于点 ,
,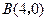 ,与y轴交于点
,与y轴交于点 .
.

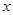 轴交于点
轴交于点 ,
, ,与y轴交于点
,与y轴交于点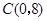 .
.
 与
与 轴的两个交点为A、B,与
轴的两个交点为A、B,与 轴交于点C
轴交于点C