题目内容
请你先将式子| 2008a |
| a2-2a+1 |
| 1 |
| a-1 |
分析：先对a2-2a+1分解因式，再进行通分化简求值．首先要弄清楚运算顺序，先去括号，再进行分式的乘除．
解答：解：原式=
÷
=
×
=
，
取a=2，原式=2008．
取a=3，原式=1004．
| 2008a |
| (a-1)2 |
| a-1+1 |
| a-1 |
=
| 2008a |
| (a-1)2 |
| a-1 |
| a |
=
| 2008 |
| a-1 |
取a=2，原式=2008．
取a=3，原式=1004．
点评：本题的关键是化简，然后把给定的值代入求值，注意给定的值一定满足式子的分母不为0．
练习册系列答案
相关题目
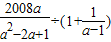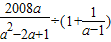化简，然后从1，2，3中选择一个数作为a的值代入其中求值．
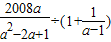化简，然后从1，2，3中选择一个数作为a的值代入其中求值．
化简，然后从1，2，3中选择一个数作为a的值代入其中求值．
化简，然后从1，2，3中选择一个数作为a的值代入其中求值．