Question

【题目】△ABC和△ADE都是等腰直角三角形， ∠BAC=∠DAE=90°.

（1）如图1，点D，E在AB，AC上，则BD，CE满足怎样的数量关系和位置关系?(直接写出答案)

（2）如图2，点D在△ABC内部， 点E在△ABC外部，连结BD， CE， 则BD，CE满足怎样的数量关系和位置关系?请说明理由.

（3）如图3，点D，E都在△ABC外部，连结BD， CE， CD， EB，BD， 与CE相交于H点.

①若BD=，求四边形BCDE的面积；

②若AB=3，AD=2，设CD2=x，EB2=y，求y与x之间的函数关系式.

Answer 1

【答案】（1）BD=CE，BD⊥CE；

（2）BD⊥CE，理由见解析；

（3）①S四边形BCDE=；②y=26-x

【解析】试题分析：（1）由等腰直角三角形的性质即可得出；

（2）由边角边证得△ABD≌△ACE，由全等三角形的性质得出∠ABD=∠ACE，延长BD，由三角形内角和即可得∠CGF=∠BAF=90°，即可证得垂直；

（3）①易证△ABD≌△ACE，可得∠BHC=∠BAC=90°，即BD⊥CE，即可求得四边形BCDE的面积；

②由勾股定理等量代换即可求得y与x之间的函数关系式.

试题解析：（1）∵△ABC和△ADE都是等腰直角三角形，

∴AB=AC.AD=AE，

∴AB-AD=AC-AE，即：BD=CE，

∵BD、CE相交于点A，∠BAC=90°，

∴BD⊥CE；

(2)∵△ABC和△ADE都是等腰直角三角形，

∴AB=AC，AD=AE，∠BAC=∠DAE=90°，

∵∠BAD=∠BAC-∠DAC， ∠CAE=∠DAE-∠DAC，

∴∠BAD=∠CAE，

∴△ABD≌△ACE，

∴BD=CE，

延长BD，分别交AC，CE于F，G，BD=CE，

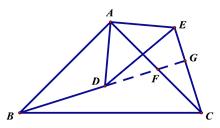
∵△ABD≌△ACE，

∴∠ABD=∠ACE，

∵∠AFB=∠GFC，

∴∠CGF=∠BAF=90°，即BD⊥CE；

（3）∵△ABC和△ADE都是等腰直角三角形，

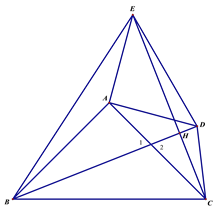
∴AB=AC，AD=AE，∠BAC=∠DAE=90°，

∵∠BAD=∠BAC+∠DAC，∠CAE=∠DAE+∠DAC，

∴∠BAD=∠CAE，

∴△ABD≌△ACE，

∴BD=CE，∠ABD=∠ACE

∵∠1=∠2

∴∠BHC=∠BAC=90°

∴S四边形BCDE=S△BCE+S△DCE= = =，

∵∠BHC=90°，

∴CD2+EB2=CH2+HD2+EH2+HB2=CH2+HB2+EH2+HD2=BC2+DE2=()2+()2=26，

∴y=26-x.