Question

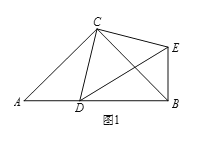
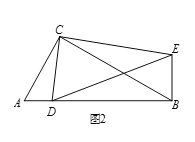
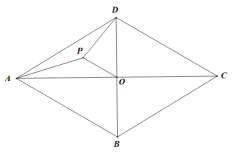
【题目】如图，在等腰中，，，将绕点逆时针旋转，得到，连结．

（1）求证：；

（2）四边形是什么形状的四边形？并说明理由；

（3）直接写出：当分别是多少度时，①；②．

Answer 1

【答案】（1）见解析；（2）四边形ABED是菱形．理由见解析；（3）① α＝30°；② α＝60°

【解析】

（1）由旋转的性质可得∠EAC=2α，∠DAE=∠BAC=α，由“SAS”可证△ABE≌△ABC，可得BE=BC；
（2）由旋转的性质可得AD=AB，BC=DE，且AB=BC，BE=BC，可证四边形ABED是菱形；
（3）由菱形的性质可求解．

（1）证明：∵将△ABC绕点A逆时针旋转2，

根据旋转的性质得：
∴∠EAC=2，∠DAE=∠BAC=，AD=AB，AE=AC，

∴∠BAE=∠EAC-∠BAC=2 - =，
∴∠BAE=∠BAC，
∵AE=AC，AB=AB，
∴△ABE≌△ABC（SAS），
∴BE=BC；
（2）答：四边形ABED是菱形．
理由如下：
∵将△ABC绕点A逆时针旋转2，
∴AD=AB，BC=DE，
∵AB=BC，BE=BC，
∴AD=AB=BE=DE，
∴四边形ABED是菱形；
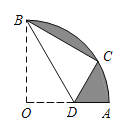
（3）如图，当BE⊥AC时，延长EB交AC于H，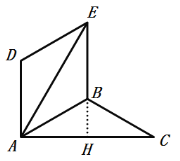

∵四边形ABED是菱形，
∴AD∥BE，
∵BE⊥AC，
∴AD⊥AC，
∴∠DAC=90°，
∵∠DAE=∠BAC=，∠EAC=2，
∴ +2 =90°，
∴ =30°；
如图，当BE∥AC，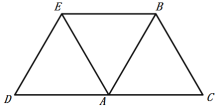

∵四边形ABED是菱形，
∴AD∥BE，
又∵BE∥AC，
∴AD与AC共线，
∴∠DAE+∠EAC=180°，
∴ +2 =180°，
∴ =60°．