题目内容
一名射击运动员在一次训练中连续射击20次，命中的环数和次数如下表所示（单位：环）：
| 命中环数 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 3 | 1 | 11 | 3 | 2 |
解：由题意可知：6环所占的百分比为3÷20=15%，对应的圆心角=360°×15%=54°，
7环所占的百分比为1÷20=5%，对应的圆心角=360°×5%=18°，
8环所占的百分比为11÷20=55%，对应的圆心角=360°×55%=198°，
9环四欧洲的百分比为3÷20=15%，对应的圆心角=360°×15%=54°，
10环所占的百分比为2÷20=10%，对应的圆心角=360°×10%=36°；
该运动员的平均成绩为
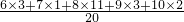=8环；该运动员命中环数的众数为8（环），则据此估计运动员在比赛中如果发挥正常，最多能射出8环的成绩．
分析：计算出命中的环数的比例及对应的圆心角，根据平均数的概念求平均环数．
点评：本题考查平均数的求法、众数的意义以及扇形统计图的制作．
练习册系列答案
相关题目
一名射击运动员在一次射击比赛中，10发子弹有2发命中10环，2发命中9环，6发命中8环．则下列说法中正确的是（ ）
| A、命中环数的平均数是9环 | B、命中环数的中位数是10环 | C、命中环数的众数是10环 | D、命中环数的中位数是8环 |
一名射击运动员在一次训练中连续射击20次，命中的环数和次数如下表所示（单位：环）：
请根据上表制成扇形统计图，并计算这名运动员的平均成绩是多少？再结合统计图，估计该运动员在比赛中如果发挥正常，最多能射出多少环的成绩．
| 命中环数 | 6 | 7 | 8 | 9 | 10 |
| 次数 | 3 | 1 | 11 | 3 | 2 |