Question

在直角坐标系中，用线段顺次连接点（-2，0），（0，3），（3，3），（4，0）．
（1）这是一个什么图形；
（2）求出它的面积；
（3）求出它的周长．

Answer 1

分析：（-2，0）和（4，0）的纵坐标相同．（0，3）和（3，3）的纵坐标相同，因而BC∥AD，BC=6，因而这个四边形是梯形，就可以进而求出面积以及周长．

解答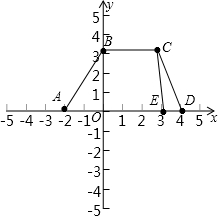：解：
（1）（0，3）和（3，3）的纵坐标相同，因而BC∥AD因而四边形ABCD是梯形．
（2）BC=3，AD=6，高OB=3，因而梯形的面积是

1

2

（3+6）×3=

27

2

．
（3）在直角三角形ABO中根据勾股定理得到AB=

13

，同理可以得到CD=

10

，因而梯形的周长是9+

10

+

13

．

点评：本题考查与梯形有关的问题，梯形的问题可以转化为解直角三角形的问题．