Question

我们知道，含有36°的等腰三角形是特殊的三角形，通常把有一个内角等于36°的三角形称为“黄金三角形”．
（1）如图1、2，在△ABC中，已知：AB=AC，且∠A=36°．请你设计两种不同的分法，将黄金三角形ABC分割成三个等腰三角形（分别画在图1，图2上）
（2）如图3，在△ABC中，已知：AB=AC，且∠B=36°．请你设计一种分法，将黄金三角形ABC分割成三个等腰三角形．（画在图3上）
注：（画图工具不限，要求画出分割线段；标出能够说明不同分法所得三角形的内角度数，不要求写画法，不要求证明．）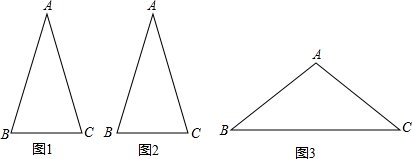

Answer 1

解：（1）如图所示：

（2）如图所示：

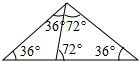
分析：（1）黄金三角形是一个等腰三角形，它的顶角为36°，每个底角为72°．它的腰与它的底成黄金比．当底角被平分时，角平分线分对边也成黄金比，并形成两个较小的等腰三角形．这两三角形之一相似于原三角形．依此作图即可．
（2）把等腰直角三角形分为两个小的等腰直角三角形即可，把108°的角分为36°和72°即可．
点评：本题考查了黄金三角形，注意线段的黄金分割点的概念的延伸，能够根据黄金分割的定义结合三角形进行分析证作图．