题目内容
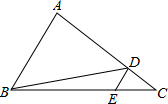 如图,已知DB平分∠ADE,DE∥AB,∠CDE=82°,则∠EDB=
如图,已知DB平分∠ADE,DE∥AB,∠CDE=82°,则∠EDB=49
49
度,∠A=82
82
度.分析:由DE∥AB,根据平行线的性质得到∠A=∠CDE,∠A+∠ADE=180°,而∠CDE=82°,则∠A=82°,∠ADE=180°-82°=98°,然后根据角平分线的定义得∠EDB=
∠ADE,即可计算出∠EDB的度数.
| 1 |
| 2 |
解答:解:∵DE∥AB,
∴∠A=∠CDE,∠A+∠ADE=180°,
∵∠CDE=82°,
∴∠A=82°,
∴∠ADE=180°-82°=98°,
又∵DB平分∠ADE,
∴∠EDB=
∠ADE=
×98°=49°.
故答案为49,82.
∴∠A=∠CDE,∠A+∠ADE=180°,
∵∠CDE=82°,
∴∠A=82°,
∴∠ADE=180°-82°=98°,
又∵DB平分∠ADE,
∴∠EDB=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为49,82.
点评:本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补.也考查了角平分线的定义.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
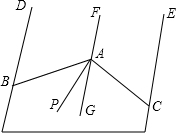 如图,已知DB∥FG∥EC,∠ABD=84°,∠ACE=60°,AP是∠BAC的平分线.求∠PAG的度数.
如图,已知DB∥FG∥EC,∠ABD=84°,∠ACE=60°,AP是∠BAC的平分线.求∠PAG的度数. 如图,已知DB平分∠ADE,DE∥AB,∠CDE=82°,则∠ABD=
如图,已知DB平分∠ADE,DE∥AB,∠CDE=82°,则∠ABD= 如图,已知DB平分∠ADE,DE∥AB,∠CDE=82°,则∠ABD=________.
如图,已知DB平分∠ADE,DE∥AB,∠CDE=82°,则∠ABD=________.