题目内容
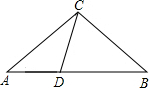（2004•广安）如图，D是△ABC的AB边上一点，连接CD，如果∠B=∠ACD，AC=6cm，AD=4cm，那么AB=9
9
cm．分析：由∠B=∠ACD，∠A是公共角，可证得△ACD∽△ABC，又由AC=6cm，AD=4cm，根据相似三角形的对应边成比例，即可求得答案．
解答：解：∵∠B=∠ACD，∠A是公共角，
∴△ACD∽△ABC，
∴
=
，
∵AC=6cm，AD=4cm，
∴AB=
=
=9（cm）．
故答案为：9．
∴△ACD∽△ABC，
∴
| AC |
| AB |
| AD |
| AC |
∵AC=6cm，AD=4cm，
∴AB=
| AC2 |
| AD |
| 62 |
| 4 |
故答案为：9．
点评：此题考查了相似三角形的判定与性质．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
开心练习课课练与单元检测系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
相关题目
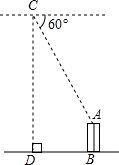（2004•广安）如图，一架巡逻的直升飞机，在距地面800米高空的C处测得经贸大厦楼顶的俯角为60°，已知此时飞机距经贸大厦的水平距离（即图中DB）为400米，试求经贸大厦的高AB（精确到1米； 参考数据：
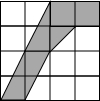（2004•广安）如图是由4×4块面积都是10的相同小矩形组成的图形，图中阴影部分的面积是
（2004•广安）如图，直线