题目内容
已知等腰三角形三边的长为a、b、c,且a=c.若关于x的一元二次方程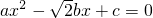 的两根之差为
的两根之差为 ,则等腰三角形的一个底角是
,则等腰三角形的一个底角是
- A.15°
- B.30°
- C.45°
- D.60°
B
分析:根据一元二次方程的根与系数的关系得到,两根之和与两根之积,把两根之差变形成与两根之和和两根之积有关的式子,代入两根之和与两根之积,得到a、b的关系后,再根据特殊角的三角函数值求得底角的度数.
解答:由根与系数的关系可知:x1+x2=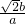 ,x1•x2=
,x1•x2= ,
,
又知(x1-x2)= ,
,
则(x1-x2)2=2,
即(x1+x2)2-4x1•x2=2,
∴2×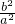 -4×
-4× =2,
=2,
解得b= a,
a,
∴底角的余弦= =
= ,
,
∴底角为30度.
故本题选B.
点评:将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
本题考查了一元二次方程的根与系数的关系,特殊角的三角函数值.
分析:根据一元二次方程的根与系数的关系得到,两根之和与两根之积,把两根之差变形成与两根之和和两根之积有关的式子,代入两根之和与两根之积,得到a、b的关系后,再根据特殊角的三角函数值求得底角的度数.
解答:由根与系数的关系可知:x1+x2=
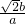 ,x1•x2=
,x1•x2= ,
,又知(x1-x2)=
 ,
,则(x1-x2)2=2,
即(x1+x2)2-4x1•x2=2,
∴2×
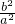 -4×
-4× =2,
=2,解得b=
 a,
a,∴底角的余弦=
 =
= ,
,∴底角为30度.
故本题选B.
点评:将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
本题考查了一元二次方程的根与系数的关系,特殊角的三角函数值.

练习册系列答案
相关题目
已知等腰三角形三边的长为a、b、c,且a=c.若关于x的一元二次方程ax2-
bx+c=0的两根之差为
,则等腰三角形的一个底角是( )
| 2 |
| 2 |
| A、15° | B、30° |
| C、45° | D、60° |
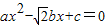 的两根之差为
的两根之差为 ,则等腰三角形的一个底角是( )
,则等腰三角形的一个底角是( )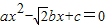 的两根之差为
的两根之差为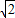 ,则等腰三角形的一个底角是( )
,则等腰三角形的一个底角是( )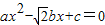 的两根之差为
的两根之差为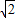 ,则等腰三角形的一个底角是( )
,则等腰三角形的一个底角是( )