题目内容
如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E,GB=8cm,AG=1cm,DE=2cm,则EF= cm.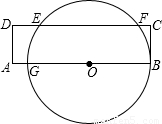
【答案】分析:过O作OW⊥CD,垂足为W,根据矩形的对称性及垂径定理即可求出EF的长.
解答: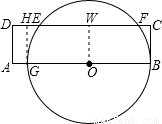 解:作GH⊥CD,交CD于点H,OW⊥CD,交CD于点W,
解:作GH⊥CD,交CD于点H,OW⊥CD,交CD于点W,
则四边形HCBG,AGHD,OWDA,OWCB都是矩形,
∵矩形HCBG是轴对称图形,对称轴是OW,
且GB是直径,
∴OG=OB= BG=4cm,
BG=4cm,
∴HW与WC是对称线段,有WH=WC,
则垂径定理知,
点W是EF的中点,
有EW=WF,
∴CH=BG=2HW=8cm,OA=WD=OG+AG=5cm,
∴EW=DW-DE=5-2=3cm,
∴EF=6cm.
点评:本题利用了垂径定理和矩形的性质:矩形是轴对称图形求解.
解答:
 解:作GH⊥CD,交CD于点H,OW⊥CD,交CD于点W,
解:作GH⊥CD,交CD于点H,OW⊥CD,交CD于点W,则四边形HCBG,AGHD,OWDA,OWCB都是矩形,
∵矩形HCBG是轴对称图形,对称轴是OW,
且GB是直径,
∴OG=OB=
 BG=4cm,
BG=4cm,∴HW与WC是对称线段,有WH=WC,
则垂径定理知,
点W是EF的中点,
有EW=WF,
∴CH=BG=2HW=8cm,OA=WD=OG+AG=5cm,
∴EW=DW-DE=5-2=3cm,
∴EF=6cm.
点评:本题利用了垂径定理和矩形的性质:矩形是轴对称图形求解.

练习册系列答案
相关题目
 如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E,GB=8cm,AG=1cm,DE=2cm,则EF=
如图,矩形ABCD与圆心在AB上的⊙O交于点G、B、F、E,GB=8cm,AG=1cm,DE=2cm,则EF=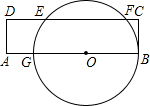 如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=8 cm,AD=2cm,则EF=
如图,矩形ABCD与圆心在AB上的⊙O交于点G,B,F,E,GB=8 cm,AD=2cm,则EF=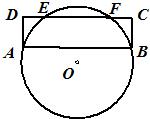 7、如图,矩形ABCD与⊙O交于点A、B、F、E,DE=1cm,EF=3cm,则AB=
7、如图,矩形ABCD与⊙O交于点A、B、F、E,DE=1cm,EF=3cm,则AB=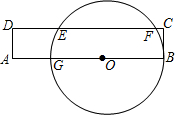 如图,矩形ABCD与圆心在AB上的圆O交于点G、B、F、E,GB=10,EF=8,那么AD=
如图,矩形ABCD与圆心在AB上的圆O交于点G、B、F、E,GB=10,EF=8,那么AD=