题目内容
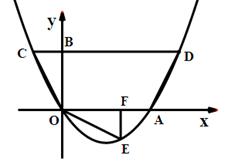
如图,抛物线![]() 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
1.求抛物线的解析式及点C的坐标
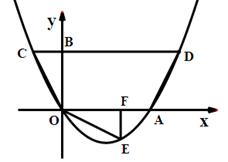
2.将△BCO绕点O按顺时针旋转90°后 再沿x轴对折得到△OEF(点C与点E对应),判断点E是否落在抛物线上,并说明理由;
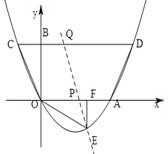
3.设过点E的直线交OA于点P,交CD边于点Q. 问是否存在点P,使直线PQ分梯形AOCD的面积为1∶3两部分?若存在,求出P点坐标;若不存在,请说明理由.
1.![]() ;C(-1,2)
;C(-1,2)
2.点E落在抛物线上. 理由如下:
![]()
由旋转、轴对称的性质知:![]()
![]() 点E点的坐标为(2,-1)
点E点的坐标为(2,-1)
当![]() 时,
时,![]()
 点E落在抛物线上.
点E落在抛物线上.
3.存在点P(a,0). 如上图记S梯形CQPO=S1,S梯形ADQP = S2,易求S梯形ABCD = 8.
当PQ经过点F(3,0)时,易求S1=5,S2 = 3,此时S1∶S2不符合条件,故a≠3.
设直线PQ的解析式为y = kx+b(k≠0),则![]() ,解得
,解得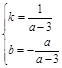 ,
,
∴![]() . 由y = 2得x = 3a-6,∴Q(3a-6,2)
. 由y = 2得x = 3a-6,∴Q(3a-6,2)
∴CQ = 3a-5,P O= a,![]() .
.
下面分两种情形:①当S1∶S2= 1∶3时,![]() = 2;
= 2;
∴4a-75= 2,解得![]() ;
;
②当S1∶S2= 3∶1时,![]() ; ∴4a-75= 6,解得
; ∴4a-75= 6,解得![]() ;
;
综上所述:所求点P的坐标为(![]() ,0)或(
,0)或(![]() ,0)
,0)
解析:(1)根据O、D两点的坐标求出抛物线的解析式,然后利用抛物线的性质求出C点的坐标;
(2)利用旋转、轴对称的性质求出E点的坐标,从而得出点E在抛物线上;
(3)分二种情况讨论:①梯形COPQ面积:梯形DAPQ面积=1:3,②梯形COPQ面积:梯形DAPQ面积=3:1.

 阅读快车系列答案
阅读快车系列答案
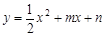 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.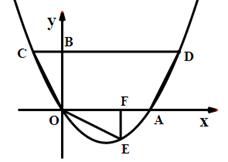
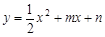 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.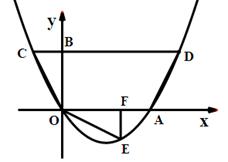
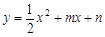 过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.
过原点O,与x轴交于A,点D(4,2)在该抛物线上,过点D作CD∥x轴,交抛物线于点C,交y轴于点B,连结CO、AD.