题目内容
If the equation m(x-1)=2001-n(x-2)for x has infinite roots,then m2001+n2001=分析:先把m(x-1)=2001-n(x-2)进行化简,然后根据方程根的个数列出方程组,解出m、n的值,最后把m、n的值代入求出结果即可.
解答:解:m(x-1)=2001-n(x-2),
mx-m=2001-nx+2n,
mx+nx=2001+2n+m,
m+n)x=2001+2n+m,
因为x有无数个根,所以
,
解得:
,
所以m2001+n2001=20012001+(-2001)2001=0.
故答案为0.
mx-m=2001-nx+2n,
mx+nx=2001+2n+m,
m+n)x=2001+2n+m,
因为x有无数个根,所以
|
解得:
|
所以m2001+n2001=20012001+(-2001)2001=0.
故答案为0.
点评:本题主要通过一元一次方程的解的个数列出二元一次方程组,在解题时要注意一元一次方程的解的灵活应用,化简时要注意结果的符号.

练习册系列答案
相关题目
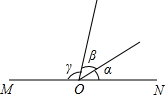 In the figure 5,MON is a atyaight line,If the angles α、βandγ,satisfy β:α=2:1,andγ:β=3:1,then the angle β=
In the figure 5,MON is a atyaight line,If the angles α、βandγ,satisfy β:α=2:1,andγ:β=3:1,then the angle β=