题目内容
△ABC≌△EFC，AB=11，BC=4，△EFC的周长为偶数，则EC的取值为________．
9或11或13
分析：先根据全等三角形对应边相等求出EF、FC，根据三角形的任意两边之和大于第三边两边之差小于第三边求出EC的取值范围，再根据周长是偶数确定出EC的长．
解答：∵AB=11，BC=4，
∴EF=AB=11，FC=BC=4，
∵11-4=7，11+4=15，
∴7＜EC＜15，
∵△EFC的周长为偶数，
∴EC为奇数，长为9或11或13．
故答案为：9或11或13．
点评：本题考查了全等三角形的性质，三角形的三边关系，主要利用了全等三角形对应边相等的性质，根据三边关系求出EC的长是解题的关键．
分析：先根据全等三角形对应边相等求出EF、FC，根据三角形的任意两边之和大于第三边两边之差小于第三边求出EC的取值范围，再根据周长是偶数确定出EC的长．
解答：∵AB=11，BC=4，
∴EF=AB=11，FC=BC=4，
∵11-4=7，11+4=15，
∴7＜EC＜15，
∵△EFC的周长为偶数，
∴EC为奇数，长为9或11或13．
故答案为：9或11或13．
点评：本题考查了全等三角形的性质，三角形的三边关系，主要利用了全等三角形对应边相等的性质，根据三边关系求出EC的长是解题的关键．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
16、如图，若△ABC≌△EFC，那么BC=
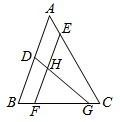如图表示D、E、F、G四点在△ABC三边上的位置，其中. |
| DG |
. |
| EF |
| A、△BDG，△CEF |
| B、△ABC，△CEF |
| C、△ABC，△BDG |
| D、△FGH，△ABC |
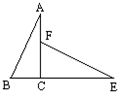如图所示，若△ABC≌△EFC，且CF=3厘米，∠EFC=64°，则BC=
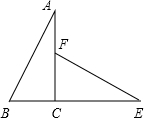如图，若△ABC≌△EFC，且CF=3cm，CE=6cm，则AF=