题目内容
将直径为60cm的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），那么每个圆锥容器的底面半径为（ ）
分析：将直径为60cm的圆形铁皮，做成三个相同的圆锥容器的侧面（不浪费材料，不计接缝处的材料损耗），则每个侧面用圆的
，则圆锥的底面周长等于圆形铁皮的周长的
，根据圆的周长公式即可求解．
| 1 |
| 3 |
| 1 |
| 3 |
解答：解：圆形铁皮的周长是：60πcm．
设每个圆锥容器的底面半径为r，则
×60π=2πr，
∴r=10cm．
故选A．
设每个圆锥容器的底面半径为r，则
| 1 |
| 3 |
∴r=10cm．
故选A．
点评：本题考查了圆锥的计算，理解圆锥的底面周长等于圆形铁皮的周长的
，是关键．
| 1 |
| 3 |
练习册系列答案
长江作业本同步练习册系列答案
相关题目
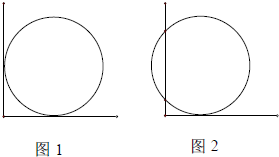（2008•高淳县二模）如图1，把圆形井盖卡在角尺〔角的两边互相垂直，一边有刻度）之间，即圆与两条直角边相切，现将角尺向右平移10cm，如图2，OA边与圆的两个交点对应CD的长为40cm，则可知井盖的直径是（ ）
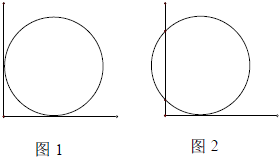如图1，把圆形井盖卡在角尺〔角的两边互相垂直，一边有刻度）之间，即圆与两条直角边相切，现将角尺向右平移10cm，如图2，OA边与圆的两个交点对应CD的长为40cm，则可知井盖的直径是