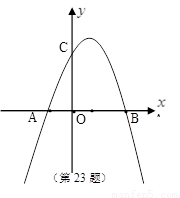题目内容
如图,已知抛物线![]() 与
与![]() 轴交于A、B两点,与
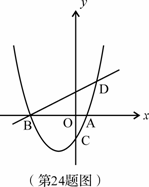
轴交于A、B两点,与![]() 轴交于C点,直线BD交抛物线于点D,并且
轴交于C点,直线BD交抛物线于点D,并且![]() (2,3),
(2,3), ![]() .
.
(1)求抛物线的解析式;
(![]() 2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,![]() 为半径且与直线 AC相切的圆,若存在,求出圆心Q的坐标,若不存在,请说明理由.
为半径且与直线 AC相切的圆,若存在,求出圆心Q的坐标,若不存在,请说明理由.
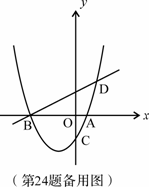
解:(1)过D作![]() 于N,
于N, ![]()
![]() D(2,3),
D(2,3),![]()
![]() ,
,![]()
![]() B(-4,0)
B(-4,0)
把B(-4,0),D(2,3)代入![]()
![]() 得
得![]() ,
,![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
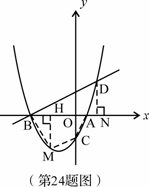
(2)过M作![]() 于
于![]() ,设
,设![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 时,S有最大值9
时,S有最大值9
(3)如右图
设AC所在直线的解析式为![]()
![]() A(1,0)
A(1,0)
![]()
![]() 所在直线的解析式为
所在直线的解析式为![]()
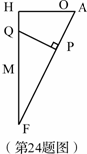 设直线AC与HM交于F,
设直线AC与HM交于F,![]() F(-2,-6)
F(-2,-6)
![]()
![]()
设![]() 与直线AC相切于P 则
与直线AC相切于P 则![]()
设Q(-2,n),![]()
![]()
![]() ∽
∽![]()
![]()
![]()
即![]() 化简得:
化简得:![]()
![]() 或
或![]()
![]() 满足条件的点Q存在,其坐标为Q(
满足条件的点Q存在,其坐标为Q(![]() 2,
2,![]() 1)或(
1)或(![]() 2,4)
2,4)

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
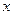 轴交于点
轴交于点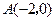 ,
,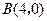 ,与
,与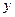 轴交于点
轴交于点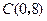 .
.
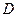 的坐标;
的坐标;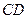 交
交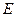 .在线段
.在线段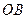 的垂直平分线上是否存在点
的垂直平分线上是否存在点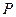 ,使得点
,使得点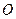 的距离?如果存在,求出点
的距离?如果存在,求出点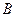 作
作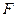 ,将抛物线沿其对称轴平移,使抛物线与线段
,将抛物线沿其对称轴平移,使抛物线与线段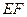 总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
总有公共点.试探究:抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?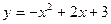 与
与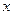 轴的两个交点为A、B,与
轴的两个交点为A、B,与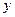 轴交于点C
轴交于点C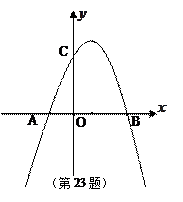
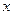 轴交于点
轴交于点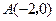 ,
,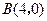 ,与y轴交于点
,与y轴交于点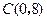 .
.

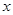 轴交于点
轴交于点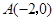 ,
,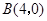 ,与y轴交于点
,与y轴交于点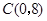 .
.
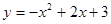 与
与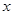 轴的两个交点为A、B,与
轴的两个交点为A、B,与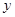 轴交于点C
轴交于点C