题目内容
【题目】直线l1:y=kx+b与直线l2:y=2x﹣4的交点M的纵坐标为2,且与直线y=﹣x﹣2交x轴于同一点.
(1)求直线l1的表达式;
(2)在给出的平面直角坐标系中作出直线l1的图象,并求出它与直线l2及x轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>0>2x﹣4的解集
【答案】(1)![]() ;(2)4;(3)﹣2<x<2
;(2)4;(3)﹣2<x<2
【解析】
(1)首先求出M的坐标,然后利用待定系数法求解析式即可;
(2)首先画出直线l1的图象,然后根据图象上的坐标即可求出面积;
(3)直接观察图象,即可得出不等式解集.
(1)由已知可得M(3,2),
直线y=﹣x﹣2与x轴的交点坐标为(﹣2,0),
由题意,可知直线l1经过点(3,2)、(﹣2,0),
则有![]() ,
,
∴![]() ,
,
∴y=![]() x+
x+![]() ;
;
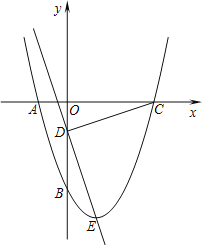
(2)如图所示:
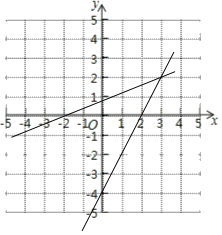
∵l1与x轴交点坐标为(﹣2,0),
直线l2:y=2x﹣4与x轴交点坐标为(2,0),
∴S=![]() ×(2+2)×2=4;
×(2+2)×2=4;
(3)由图象可得不等式解集为﹣2<x<2;

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目