题目内容
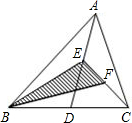
 如图△ABC中,已知D、E、F分别是BC、AD、CE的中点,且S△ABC=4,那么阴影部分的面积等于
如图△ABC中,已知D、E、F分别是BC、AD、CE的中点,且S△ABC=4,那么阴影部分的面积等于
- A.2
- B.1
- C.

- D.

B
分析:如图,因为点F是CE的中点,所以△BEF的底是△BEC的底的一半,△BEF高等于△BEC的高;同理,D、E、分别是BC、AD的中点,△EBC与△ABC同底,△EBC的高是△ABC高的一半;利用三角形的等积变换可解答.
解答:如图,点F是CE的中点,
∴△BEF的底是EF,△BEC的底是EC,即EF= EC,高相等;
EC,高相等;
∴S△BEF= S△BEC,
S△BEC,
D、E、分别是BC、AD的中点,同理得,
S△EBC= S△ABC,
S△ABC,
∴S△BEF= S△ABC,且S△ABC=4,
S△ABC,且S△ABC=4,
∴S△BEF=1,
即阴影部分的面积为1.
故选B.
点评:本题主要考查了三角形面积的等积变换:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.结合图形直观解答.
分析:如图,因为点F是CE的中点,所以△BEF的底是△BEC的底的一半,△BEF高等于△BEC的高;同理,D、E、分别是BC、AD的中点,△EBC与△ABC同底,△EBC的高是△ABC高的一半;利用三角形的等积变换可解答.
解答:如图,点F是CE的中点,
∴△BEF的底是EF,△BEC的底是EC,即EF=
 EC,高相等;
EC,高相等;∴S△BEF=
 S△BEC,
S△BEC,D、E、分别是BC、AD的中点,同理得,
S△EBC=
 S△ABC,
S△ABC,∴S△BEF=
 S△ABC,且S△ABC=4,
S△ABC,且S△ABC=4,∴S△BEF=1,
即阴影部分的面积为1.
故选B.
点评:本题主要考查了三角形面积的等积变换:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.结合图形直观解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
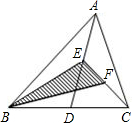 如图△ABC中,已知D、E、F分别是BC、AD、CE的中点,且S△ABC=4,那么阴影部分的面积等于( )
如图△ABC中,已知D、E、F分别是BC、AD、CE的中点,且S△ABC=4,那么阴影部分的面积等于( )| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
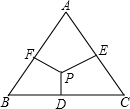 如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF=
如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF=