题目内容
如图，直y=mx与双曲线y=
交于点A，B．过点A作AM⊥x轴，垂足为点M，连接BM．若S△ABM=1，则k的值是（ ）
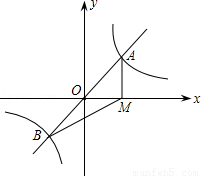
A． 1 B． m﹣1 C． 2 D． m
【答案】
A
【解析】
试题分析：利用三角形的面积公式和反比例函数的图象性质可知．
解：由图象上的点A、B、M构成的三角形由△AMO和△BMO的组成，点A与点B关于原点中心对称，
∴点A，B的纵横坐标的绝对值相等，
∴△AMO和△BMO的面积相等，且为
，
∴点A的横纵坐标的乘积绝对值为1，
又因为点A在第一象限内，
所以可知反比例函数的系数k为1．
故选A．
考点：反比例函数系数k的几何意义．
点评：本题利用了反比例函数的图象在一、三象限和S△=|xy|而确定出k的值．
练习册系列答案
相关题目
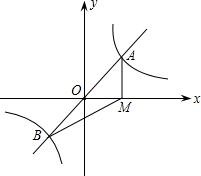如图，直y=mx与双曲线y=
交于点A，B．过点A作AM⊥x轴，垂足为点M，连接BM．若S△ABM=1，则k的值是（ ）
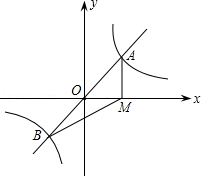
交于点A，B．过点A作AM⊥x轴，垂足为点M，连接BM．若S△ABM=2，则k的值是 ．
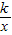交于点A，B．过点A作AM⊥x轴，垂足为点M，连接BM．若S△ABM=1，则k的值是（ ）