题目内容
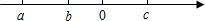 若实数a、b、c在数轴上的位置如图,则化简
若实数a、b、c在数轴上的位置如图,则化简| a2 |
| (a+b)2 |
考点:二次根式的性质与化简,实数与数轴
专题:计算题
分析:首先根据数轴得出a,b,c的符号,进而得出a+b<0,b-c<0,再利用绝对值得性质和二次根式的性质化简求出即可.
解答:解:由数轴可得出:a<b<0<c,
∴a+b<0,b-c<0,
∴
-
+|b-c|
=-a+(a+b)+c-b,
=c.
故答案为:c.
∴a+b<0,b-c<0,
∴
| a2 |
| (a+b)2 |
=-a+(a+b)+c-b,
=c.
故答案为:c.
点评:此题主要考查了实数与数轴以及二次根式和绝对值的性质,正确化简二次根式是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列说法正确的是( )
| A、点到直线的距离是指直线外的一点到这条直线的垂线的长 | |||
B、
| |||
| C、两个无理数的和一定是无理数 | |||
| D、任何实数的绝对值都是非负数 |
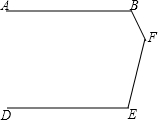 如图,如果直线AB∥DE,则∠B+∠E+∠F=
如图,如果直线AB∥DE,则∠B+∠E+∠F= 如图,∠1=∠2,∠B=57°,则∠BAD=
如图,∠1=∠2,∠B=57°,则∠BAD=