题目内容
如图,矩形![]() 是由矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,
是由矩形OABC(边OA在x轴正半轴上,边OC在y轴正半轴上)绕B点逆时针旋转得到的,![]() 点在x轴的正半轴上,B点的坐标为(1,3).
点在x轴的正半轴上,B点的坐标为(1,3).![]() 与AB交于D点.
与AB交于D点.
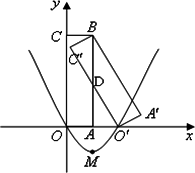
(1)求D点的坐标;
(2)如果二次函数y=ax2+bx+c(a≠0)的图象经过点O、![]() 两点且图象顶点M的纵坐标为-1,求这个二次函数的解析式;
两点且图象顶点M的纵坐标为-1,求这个二次函数的解析式;
(3)若将直线OC绕点O旋转α度(0<α<90)后与抛物线的另一个交点为P,则以O、![]() 、B、P为顶点的四边形能否是平行四边形?若能,求出tanα的值;若不能,请说明理由.
、B、P为顶点的四边形能否是平行四边形?若能,求出tanα的值;若不能,请说明理由.
答案:
解析:
解析:
|
易证△AO ∴O 设O ∴m2=(3-m)2+12 m= ∴点D(1, (2)抛物线过O(0,0), 设y=a(x-1)2-1,则a=1 ∴y=(x-1)2-1 即y=x2-2x 3分 (3)O 设P(x,3),P在抛物线上 ∴x2-2x=3 x1=-1,x2=3, ∴P(-1,3)或(3,3) 当点P(3,3)时,∠COP=α=45°,tanα=1 当点 |

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
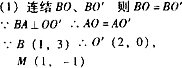
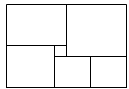
 18、如图,矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的长为
18、如图,矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的长为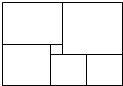 如图,矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的长为________,宽为________.
如图,矩形是由六个正方形组成,其中最小的正方形的面积为1,则此矩形的长为________,宽为________. 是由矩形
是由矩形 (边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的,
(边OA在x轴正半轴上,边OC在y轴正半轴上)绕点B逆时针旋转得到的, 点在x轴的正半轴上,B点的坐标为 (1,3),
点在x轴的正半轴上,B点的坐标为 (1,3), 与AB交于D点。
与AB交于D点。 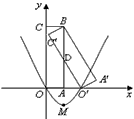
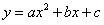 (
(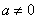 )的图象经过点O、
)的图象经过点O、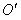 两点且图象顶点M的纵坐标为-1,求这个二次函数的解析式;
两点且图象顶点M的纵坐标为-1,求这个二次函数的解析式; 度(
度(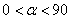 )后与抛物线的另一个交点为P,则以O、
)后与抛物线的另一个交点为P,则以O、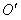 、B、P为顶点的四边形能否是平行四边形?若能,求出
、B、P为顶点的四边形能否是平行四边形?若能,求出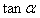 的值;若不能,请说明理由。
的值;若不能,请说明理由。