题目内容
叙述并证明“三角形的内角和定理”．（要求根据下图写出已知、求证并证明）
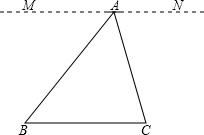证明：过点A作直线MN，使MN∥BC．∵MN∥BC，
∴∠B=∠MAB，∠C=∠NAC（两直线平行，内错角相等）
∵∠MAB+∠NAC+∠BAC=180°（平角定义）
∴∠B+∠C+∠BAC=180°（等量代换）
即∠A+∠B+∠C=180°．
分析：欲证明三角形的三个内角的和为180°，可以把三角形三个角转移到一个平角上，利用平角的性质解答．
点评：过点A作平行于BC的直线MN，两直线平行，内错角相等，通过等量代换求证定理．
练习册系列答案
相关题目
22、叙述并证明“三角形的内角和定理”．（要求根据下图写出已知、求证并证明）
已知：如图，△ABC为等腰三角形，且底角为72°．请标上字母，再根据下列叙述画图并回答问题：延长BA到D使DA=AC，连接DC．（画出所有符合题意的图形，图不够时请自己画） 