题目内容
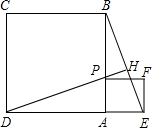 如图,若点P为正方形ABCD边AB上一点,以PA为一边作正方形AEFP,连BE、DP,并延长DP交BE于点H,求证:DH⊥BF.
如图,若点P为正方形ABCD边AB上一点,以PA为一边作正方形AEFP,连BE、DP,并延长DP交BE于点H,求证:DH⊥BF.
 解:在△PAD和△EAB中,
解:在△PAD和△EAB中,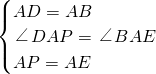 ,
,∴△PAD≌△EAB,即∠EBA=∠PDA,
又∠HDE+∠DPA=90°,∠EBA=∠PDA,∠DPA=∠BPH(对顶角相等),
∴∠EBA+∠BPH=90°,
∴∠DHB=90°,
∴DH⊥BE.
分析:先求证△PAD≌△EAB,求得∠EBA=∠PDA,根据∠HDE+∠DPA=90°,∠EBA=∠PDA,∠DPA=∠BPH,得出∠EBA+∠BPH=90°,即可得出DH⊥BF.
点评:本题考查了正方形各边长相等且各内角为直角的性质,全等三角形的判定和全等三角形对应边相等的性质,本题中正确的求∠PDA+∠EAB=90°是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
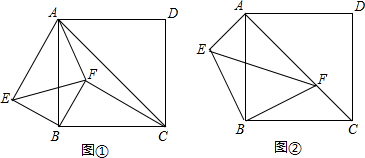

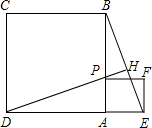 如图,若点P为正方形ABCD边AB上一点,以PA为一边作正方形AEFP,连BE、DP,并延长DP交BE于点H,求证:DH⊥BF.
如图,若点P为正方形ABCD边AB上一点,以PA为一边作正方形AEFP,连BE、DP,并延长DP交BE于点H,求证:DH⊥BF.