题目内容
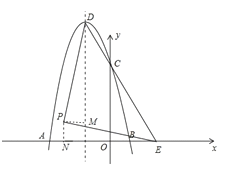
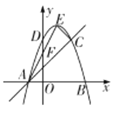
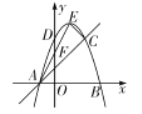
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]()
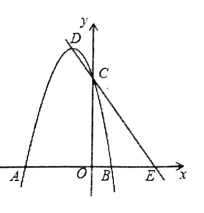
(1)求抛物线的顶点坐标(用含![]() 的式子表示);
的式子表示);
(2)![]() 的长是否与
的长是否与![]() 值有关,说明你的理由;
值有关,说明你的理由;
(3)设![]() ,求
,求![]() 的取值范围;
的取值范围;
(4)以![]() 为斜边,在直线
为斜边,在直线![]() 的左下方作等腰直角三角形
的左下方作等腰直角三角形![]() .设
.设![]() ,直接写出
,直接写出![]() 关于
关于![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.
【答案】(1)顶点D(﹣1,-4a);(2)OE=3,OE的长与a值无关,理由见解析;(3)![]() ;(4)n=﹣m﹣1(m<1),理由见解析.
;(4)n=﹣m﹣1(m<1),理由见解析.
【解析】
(1)根据待定系数法,得![]() ,从而得y=ax2+2ax-3a,进而得到顶点的坐标;
,从而得y=ax2+2ax-3a,进而得到顶点的坐标;
(2)由y=ax2+2ax﹣3a,得C(0,﹣3a),D(﹣1,﹣4a),从而得点E的坐标,即可得到结论;
(3)当β=45°时,OC=OE=3,求出a=﹣1,当β=60°时,OC=3![]() ,求出a=﹣
,求出a=﹣![]() ,进而即可求解;
,进而即可求解;
(4)作PM⊥对称轴于M,PN⊥AB于N,易证△DPM≌△EPN,得PM=PN,DM=EN,结合D(﹣1,﹣4a),E(3,0),![]() ,即可得到结论.
,即可得到结论.
(1)把![]() ,
,![]() 代入函数
代入函数![]() ,得:
,得:
![]() ,解得:
,解得:![]() ,
,
∴二次函数解析式为:y=ax2+2ax-3a,
∴顶点D(﹣1,-4a);
(2)OE的长与a值无关,理由如下:
∵y=ax2+2ax﹣3a,
∴C(0,﹣3a),
∵D(﹣1,﹣4a),
∴直线CD的解析式为:y=ax﹣3a,
∴当y=0时,x=3,
∴E(3,0),
∴OE=3,
∴OE的长与a值无关;
(3)当β=45°时,OC=OE=3,
∴﹣3a=3,
∴a=﹣1,
当β=60°时,在Rt△OCE中,OC=![]() OE=3
OE=3![]() ,
,
∴﹣3a=3![]() ,
,
∴a=﹣![]() ,
,
∴45°≤β≤60°时,a的取值范围为:![]() ;
;
(4)n=﹣m﹣1,m<1,理由如下:
作PM⊥对称轴于M,PN⊥AB于N.
∵PD=PE,∠PMD=∠PNE=90°,∠DPE=∠MPN=90°,
∴∠DPM=∠EPN,
∴△DPM≌△EPN(AAS),
∴PM=PN,DM=EN.
∵D(﹣1,﹣4a),E(3,0),![]() ,
,
∴由PM=PN,得:-1-n=m,
∴n=﹣m﹣1,
当顶点D在x轴上时,P(1,﹣2),此时m的值1.
∵抛物线的顶点在第二象限,
∴m<1,
∴n=﹣m﹣1(m<1).