题目内容
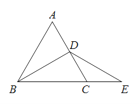
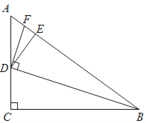
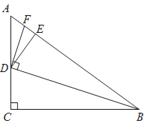
【题目】如图,△ABC中,∠ACB=90°,tanA=![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
【答案】(1)证明见解析;(2)AD2=AF·AB,理由见解析;(3)5+2![]() .
.
【解析】试题解析:(1)根据题意得∠ADF+∠BDC=∠EDF+∠BDE=90°,由折叠可知,∠BDE=∠BDC.所以∠ADF=∠EDF;
(2)易证△ADF∽△ABD,得AF∶AD=AD∶AB=DF∶DB,得AD2=AF·AB;
(3)设AE=x,DE=![]() x,由勾股定理可得,AD=DE=
x,由勾股定理可得,AD=DE=![]() x,可证△ADE∽△DFE,得BE=2x2,由(2)知AD2=AF·AB,即3x2=(x-1)×(x+2x2).解得x 的值,即可求BC的值
x,可证△ADE∽△DFE,得BE=2x2,由(2)知AD2=AF·AB,即3x2=(x-1)×(x+2x2).解得x 的值,即可求BC的值
试题解析:(1)∵DF⊥DB,∴∠BDF=90°.
∴∠ADF+∠BDC=∠EDF+∠BDE=90°
由折叠可知,∠BDE=∠BDC.
∴∠ADF=∠EDF.
(2)AD,AF,AB之间的数量关系为AD2=AF·AB,理由如下:
由折叠可知,∠DEF=∠BFD=∠C=90°.
∴∠EDF+∠DFE=∠ABD+∠DFE=90°.
∴∠EDF=∠ABD.
∴∠ADF=∠DBA.
∵∠A=∠A,∴△ADF∽△ABD.
∴AF∶AD=AD∶AB=DF∶DB.
∴AD2=AF·AB.
(3)在Rt△ADE中,tanA=DE∶AE=![]() ∶1,则可设AE=x,DE=
∶1,则可设AE=x,DE=![]() x,由勾股定理可得,AD=DE=
x,由勾股定理可得,AD=DE=![]() x.
x.
∵∠ABD=∠EDF,∠AED=∠DEF,
∴△ADE∽△DFE. ∴DE∶EF=BE∶DE,即DE2=EF·EB.
∴(![]() x)2=1×BE,即BE=2x2。
x)2=1×BE,即BE=2x2。
由(2)知AD2=AF·AB,
∴(![]() x)2=(AE-EF)(AE+BE)=(x-1)×(x+2x2).
x)2=(AE-EF)(AE+BE)=(x-1)×(x+2x2).
即3x2=(x-1)×(x+2x2).
解得,x=1+![]() ,x=1-
,x=1-![]() (舍).
(舍).
∴BE=2x2=2(1+![]() )2=5+2
)2=5+2![]() .
.
由折叠可知,BC=BE=5+2![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案