题目内容
如图,一转盘被等分成三个扇形,上面分别标有-1,1,2,指针位置固定,转动转盘后任其自由停止后,某个扇形会恰好停在指针所指的位置,得到这个扇形上相应的数.若指针恰好指在等分线上,则需重新转动转盘.
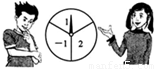
(1)若小静转动转盘一次,则她得到负数的概率为 ;
(2)小宇和小静分别转动转盘一次,若两人得到的数相同,则称两人“不谋而合”.请用列表法(或画树状图)求出两人“不谋而合”的概率.
【答案】
(1)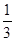 ;(2)
;(2)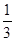
【解析】
试题分析:(1)由转盘被等分成三个扇形,上面分别标有-1,1,2,利用概率公式即可求得小静转动转盘一次,得到负数的概率;
(2)列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式:概率=所求情况数与总情况数之比,即可求出该事件的概率.
试题解析:(1)∵转盘被等分成三个扇形,上面分别标有-1,1,2,
∴小静转动转盘一次,得到负数的概率为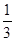 ;
;
(2)列表得:

∴一共有9种等可能的结果,
两人得到的数相同的有3种情况,
∴两人“不谋而合”的概率为 .
.
考点:用列表法或画树状图法求概率

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
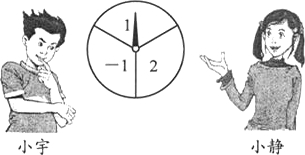
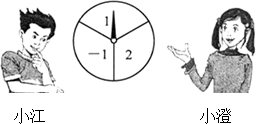 (2013•澄江县一模)如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).
(2013•澄江县一模)如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).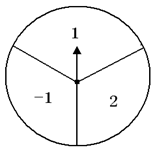
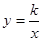 的图象在第一、三象限的概率是多少?若小静和小宇进行游戏,每人各转动两次转盘,若两次所得数的积为正数,则小静赢,若两次所得数的积为负数,则小宇赢.这是个公平的游戏吗?请说明理由.(借助画树状图或列表的方法)
的图象在第一、三象限的概率是多少?若小静和小宇进行游戏,每人各转动两次转盘,若两次所得数的积为正数,则小静赢,若两次所得数的积为负数,则小宇赢.这是个公平的游戏吗?请说明理由.(借助画树状图或列表的方法)