题目内容
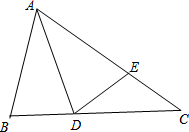 如图,△ABC中,AB=AD=AE,DE=EC,∠DAB=30°,求∠C的度数.
如图,△ABC中,AB=AD=AE,DE=EC,∠DAB=30°,求∠C的度数.考点:等腰三角形的性质
专题:
分析:首先根据AB=AD=AE,DE=EC,得到∠B=∠ADB,∠ADE=∠AED,∠C=∠EDC,从而得到∠ADE=∠AED=∠C+∠EDC=2∠C,根据∠DAB=30°,求得∠B=∠ADB=75°,利用∠ADC=∠ADE+∠EDC=3∠C=105°,求得∠C即可.
解答:解:∵AB=AD=AE,DE=EC,
∴∠B=∠ADB,∠ADE=∠AED,∠C=∠EDC,
∴∠ADE=∠AED=∠C+∠EDC=2∠C,
∵∠DAB=30°,
∴∠B=∠ADB=75°,
∴∠ADC=∠ADE+∠EDC=3∠C=105°,
∴∠C=35°.
∴∠B=∠ADB,∠ADE=∠AED,∠C=∠EDC,
∴∠ADE=∠AED=∠C+∠EDC=2∠C,
∵∠DAB=30°,
∴∠B=∠ADB=75°,
∴∠ADC=∠ADE+∠EDC=3∠C=105°,
∴∠C=35°.
点评:本题考查了等腰三角形的性质,解题的关键是利用等腰三角形的性质求得有关角的度数.

练习册系列答案
相关题目
已知点A(2,-3)和B(a,b)关于原点对称,则(a+b)2008的值为( )
| A、2008 | B、0 | C、-1 | D、1 |
已知点P1(a,b)在函数y=
(k≠0)的图象上,那么不在此图象上的点是( )
| k |
| x |
| A、P1(b,a) | ||||
| B、P2(-a,-b) | ||||
| C、P3(-b,-a) | ||||
D、P4(-
|
下列二次函数中,图象以x=-1为对称轴,且经过点(0,2)的是( )
| A、y=(x-1)2-1 |
| B、y=(x+1)2-1 |
| C、y=(x-1)2+1 |
| D、y=(x+1)2+1 |
 如图所示,△ABO≌△DCO,且AB∥CD,写出两个三角形的对应边及对应角.
如图所示,△ABO≌△DCO,且AB∥CD,写出两个三角形的对应边及对应角.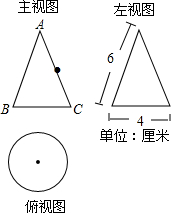 如图是一个几何体的三视图.
如图是一个几何体的三视图.