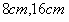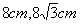题目内容
菱形的周长是32cm,一个内角的度数是60°,则两条对角线的长分别为
- A.8cm,16cm
- B.8cm,8cm
- C.
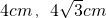
- D.
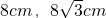
D
分析:先连接AC、BD,AC、BD交于点O,由于四边形ABCD是菱形,那么AB=BC=CD=AD,从而易求菱形的边长,再根据∠ABC=60°,有一个角是60°的等腰三角形是等边三角形可证△ABC是等边三角形,利用勾股定理可得出对角线的长度.
解答:如右图所示,∠ABC=60°,连接AC、BD,AC、BD交于点O,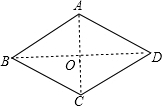
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
又∵菱形的周长为32,
∴AB=BC=CD=AD=8,
又∵∠ABC=60°,
∴△BAC是等边三角形,
∴AC=AB=6,
BO= =4
=4 ,
,
∴BD=2BO=8 ,即两条对角线分别为:8cm、8
,即两条对角线分别为:8cm、8 cm.
cm.
故选D.
点评:本题考查了菱形的性质、等边三角形的判定和性质.关键是画图,求出菱形边长,另外要掌握菱形的对角线互相垂直,利用勾股定理进行解答,难度一般.
分析:先连接AC、BD,AC、BD交于点O,由于四边形ABCD是菱形,那么AB=BC=CD=AD,从而易求菱形的边长,再根据∠ABC=60°,有一个角是60°的等腰三角形是等边三角形可证△ABC是等边三角形,利用勾股定理可得出对角线的长度.
解答:如右图所示,∠ABC=60°,连接AC、BD,AC、BD交于点O,

∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
又∵菱形的周长为32,
∴AB=BC=CD=AD=8,
又∵∠ABC=60°,
∴△BAC是等边三角形,
∴AC=AB=6,
BO=
 =4
=4 ,
,∴BD=2BO=8
 ,即两条对角线分别为:8cm、8
,即两条对角线分别为:8cm、8 cm.
cm.故选D.
点评:本题考查了菱形的性质、等边三角形的判定和性质.关键是画图,求出菱形边长,另外要掌握菱形的对角线互相垂直,利用勾股定理进行解答,难度一般.

练习册系列答案
相关题目
 cm
cm cm
cm