题目内容

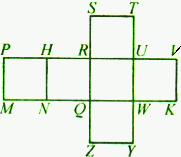
如图，这是正方体的表面展开图．如果将它还原成正方体的表面，则与点P重合的点是________．

答案：
解析：

将正方体的表面展开图还原后，面PMNH、SRUT、UWKV是有公共顶点P的3个面，所以与点P重合的点是T、V．

提示：

解此题的关键是要想像出还原后正方体的各个面与展开图中各个小正方形的对应关系．

练习册系列答案

复习计划100分期末暑假衔接中原农民出版社系列答案

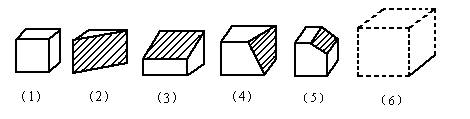
（2）观察上表，请你归纳上述各种木块的顶点数、棱数、面数之间的数量关系，这种数量关系是_________．

（3）图（6）是用虚线画出的正方体木块，请你想像一种与图（2）～（5）不同的切法，把切去一块后得到的那一块的每条棱都改成实线，则该木块的顶点数、棱数、面数分别是__________．这与你在第（2）题中归纳的关系是否相符？

（1）图（1）是正方体木块，把它切去一块，可能得到形如图（2），（3），（4）（5）的木块．

我们知道，图（1）的正方体木块有8个顶点，12条棱，6个面，请你将图（2），（3），（4），（5）中木块的顶点数，棱数，面数填入下表：
图顶点数棱数面数
（1） 8 12 6
（2）
（3）
（4）
（5）
（2）观察上表，请你归纳上述各种木块的顶点数，棱数，面数之间的数量关系，这种数量关系是：．
（3）如图，是用虚线画出的正方体木块，请你想象一种与图（2）～（5）不同的切法，把切去一块后得到的那一块的每条棱都改画成实线，则该木块的顶点数为，棱数为，面数为．这与你（2）题中所归纳的关系是否相符？

下面图1是正方体木块，若用不同的方法，把它切去一块，可以得到如图2、图3、图4、图5不同形状的木块．

（1）我们知道，图1的正方体木块有8个顶点，12条棱，6个面．请你观察，将图2、图3、图4、图5中木块的顶点数a、棱数b、面数c填入下表：

（2）观察这张表，请你归纳出上述各种木块的顶点数a、棱数b、面数c之间的数量关系，这种数量是：（用含a、b、c的一个等式表示）．