题目内容
若A=(2+1)(22+1)(24+1)(28+1),则A-2003的末位数字是( ).
| A.0 | B.2 | C.4 | D.6 |
B
试题分析:仔细分析A式子的特征可把A式子的最前面乘以
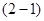 ,再根据平方差公式求解即可.
,再根据平方差公式求解即可.A=(2+1)(22+1)(24+1)(28+1)
=(2-1)(2+1)(22+1)(24+1)(28+1)
=(22-1)(22+1)(24+1)(28+1)
=(24-1)(24+1)(28+1)
=(28-1)(28+1)
=216-1
因为216-1的末位数字是5
所以A-2003=216-1-2003的末位数字是2
故选B.
点评:解题的关键是熟练掌握平方差公式:
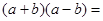
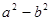 .
.
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
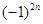 =______,
=______,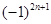 =______.
=______.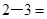
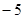
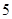
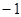
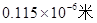
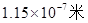
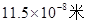
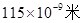
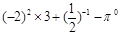 ;
;