题目内容
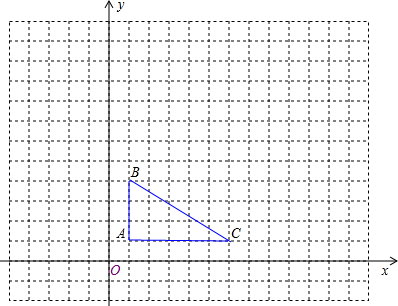
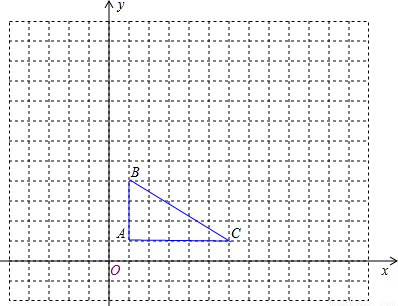
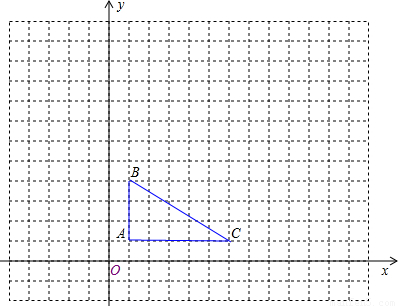
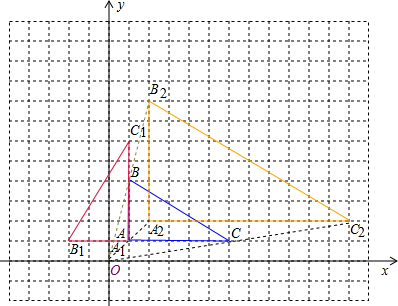
如图所示,在14×18的网格中建立平面直角坐标系,△ABC的顶点在格点上,点A的坐标为(1,1).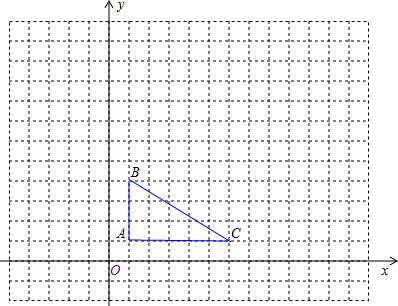
(1)把△ABC绕点A按逆时针方向旋转90°后得到△AB1C1,请画出△AB1C1的图形,并写出C1的坐标;
(2)把△ABC以点O为位似中心放大,使放大前后对应边的比为1﹕2,在第一象限内画出放大后的△A2B2C2的图形.
分析:(1)由把△ABC绕点A按逆时针方向旋转90°后得到△AB1C1可得AB⊥AB1,AC⊥AC1,BC⊥B1C1,AB=AB1,AC=AC1,BC=B1C1,由此可画出△AB1C1;
(2)由把△ABC以点O为位似中心放大,使放大前后对应边的比为1:2,可得出:△OAC∽△OA2B2,△OAB∽△OA2B2,且相似比为1:2;AC∥A2C2,AB∥A2B2,AC=
A2C2,AB=
A2B2;由此可画出△A2B2C2
(2)由把△ABC以点O为位似中心放大,使放大前后对应边的比为1:2,可得出:△OAC∽△OA2B2,△OAB∽△OA2B2,且相似比为1:2;AC∥A2C2,AB∥A2B2,AC=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵把△ABC绕点A按逆时针方向旋转90°后得到△AB1C1
∴AB⊥AB1,AC⊥AC1,BC⊥B1C1,
AB=AB1,AC=AC1,BC=B1C1
如图所示,△AB1C1就是所要画的三角形
由图形可看出,C1(1,6);
(2)∵把△ABC以点O为位似中心放大,使放大前后对应边的比为1﹕2
∴△OAC∽△OA2B2,△OAB∽△OA2B2,且相似比为1:2;
AC∥A2C2,AB∥A2B2,AC=
A2C2,AB=
A2B2
如图所示,△A2B2C2就是所要画的三角形.
∴AB⊥AB1,AC⊥AC1,BC⊥B1C1,
AB=AB1,AC=AC1,BC=B1C1
如图所示,△AB1C1就是所要画的三角形
由图形可看出,C1(1,6);

(2)∵把△ABC以点O为位似中心放大,使放大前后对应边的比为1﹕2
∴△OAC∽△OA2B2,△OAB∽△OA2B2,且相似比为1:2;
AC∥A2C2,AB∥A2B2,AC=
| 1 |
| 2 |
| 1 |
| 2 |
如图所示,△A2B2C2就是所要画的三角形.
点评:本题考查了旋转变换和位似变换后图形的画法.

练习册系列答案
相关题目
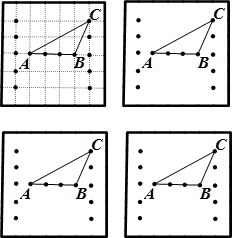 21、如图所示,在7×6的正方形网格中,选取14个格点,以其中三个格点为顶点一画出△ABC,请你以选取的格点为顶点再画出一个三角形,且分别满足下列条件:
21、如图所示,在7×6的正方形网格中,选取14个格点,以其中三个格点为顶点一画出△ABC,请你以选取的格点为顶点再画出一个三角形,且分别满足下列条件: