Question

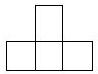7、在6×6的棋盘上剪下一个由四个小方格组成的凸字形，如图，有多少种不同的剪法？

Answer 1

分析：把凸字形分为两类，第一类：凸字形的头在棋盘的边框，但是棋盘的四个角是不能充当凸字形的头的；
第二类：凸字形的头在棋盘的内部，棋盘内部的每一个小方格可以作为4个凸字形的头（即头朝上，头朝下，头朝左，头朝右），分别求出各类出现的个数，再把两类相加即可．

解答：解：我们把凸字形上面那个小方格称为它的头，每个凸字形有并且只有一个头．
凸字形可以分为两类：
第一类：凸字形的头在棋盘的边框，但是棋盘的四个角是不能充当凸字形的头的．于是，边框上（不是角）的小方格共有4×4=16个，每一个都是一个凸字形的头，
所以，这类凸字形有16个．
第二类：凸字形的头在棋盘的内部，棋盘内部的每一个小方格可以作为4个凸字形的头（即头朝上，头朝下，头朝左，头朝右），
所以，这类凸字形有4×（4×4）=64（个）．
由加法原理知，有16+64=80种不同的凸字形剪法．
故答案为：80种．

点评：本题考查的是加法原理与乘法原理，分别列举出可能出现的两种情况是解答此题的关键．