题目内容
【题目】如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF. 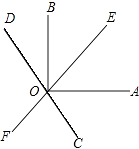
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数.(用含α的代数式表示)
【答案】
(1)解:∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,
∴∠AOF=140°;
又∵OC平分∠AOF,
∴∠FOC= ![]() ∠AOF=70°,
∠AOF=70°,
∴∠EOD=∠FOC=70°(对顶角相等);
∵∠BOE=∠AOB﹣∠AOE=50°,
∴∠BOD=∠EOD﹣∠BOE=20°
(2)解:∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,
∴∠AOF=180°﹣α;
又∵OC平分∠AOF,
∴∠FOC= ![]() ∠AOF=90°﹣
∠AOF=90°﹣ ![]() α,
α,
∴∠EOD=∠FOC=90°﹣ ![]() α(对顶角相等);
α(对顶角相等);
∵∠BOE=∠AOB﹣∠AOE=90°﹣α,
∴∠BOD=∠EOD﹣∠BOE= ![]() α.
α.
【解析】(1)根据平角的性质求得∠AOF,又由角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;(2)根据平角的性质求得∠AOF,又由角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE.
【考点精析】通过灵活运用角的平分线和对顶角和邻补角,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个即可以解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目