题目内容
若两条平行线被第三条直线所截,则同位角的平分线互相______;内错角的平分线互相______;同旁内角的平分线互相______.
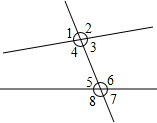
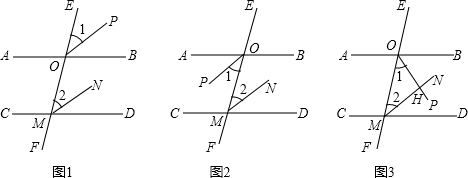
(1)如图1,AB∥CD,EF与AB、CD分别相交于点O、M,OP、MN分别是∠BOE、∠DMO的平分线.
∵AB∥CD,
∴∠BOE=∠DMO(两直线平行,同位角相等).
∵OP、MN分别是∠BOE、∠DMO的平分线,
∴∠1=
∠BOE,∠2=
∠DMO,
∴∠1=∠2,
∴OP∥MN(同位角相等,两直线平行);
(2)如图2,AB∥CD,EF与AB、CD分别相交于点O、M,OP、MN分别是∠AOM、∠DMO的平分线.
∵AB∥CD,
∴∠AOM=∠DMO(两直线平行,内错角相等).
∵OP、MN分别是∠AOM、∠DMO的平分线,
∴∠1=
∠AOM,∠2=
∠DMO,
∴∠1=∠2,
∴OP∥MN(内错角相等,两直线平行);
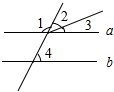
(3)如图3,AB∥CD,EF与AB、CD分别相交于点O、M,OP、MN分别是∠BOM、∠DMO的平分线,并相交于点H.
∵AB∥CD,
∴∠BOM+∠DMO=180°(两直线平行,同旁内角互补).
∵OP、MN分别是∠BOM、∠DMO的平分线,
∴∠1=
∠BOM,∠2=
∠DMO,
∴∠1+∠2=90°,
在△OMH中,
∠1+∠2+∠OHM=180°,
∴∠OHM=180°-90°=90°,
即OP⊥MN.
∵AB∥CD,
∴∠BOE=∠DMO(两直线平行,同位角相等).
∵OP、MN分别是∠BOE、∠DMO的平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2,
∴OP∥MN(同位角相等,两直线平行);
(2)如图2,AB∥CD,EF与AB、CD分别相交于点O、M,OP、MN分别是∠AOM、∠DMO的平分线.
∵AB∥CD,
∴∠AOM=∠DMO(两直线平行,内错角相等).
∵OP、MN分别是∠AOM、∠DMO的平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2,
∴OP∥MN(内错角相等,两直线平行);
(3)如图3,AB∥CD,EF与AB、CD分别相交于点O、M,OP、MN分别是∠BOM、∠DMO的平分线,并相交于点H.
∵AB∥CD,
∴∠BOM+∠DMO=180°(两直线平行,同旁内角互补).
∵OP、MN分别是∠BOM、∠DMO的平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=90°,
在△OMH中,
∠1+∠2+∠OHM=180°,
∴∠OHM=180°-90°=90°,
即OP⊥MN.


练习册系列答案
相关题目