题目内容
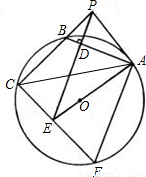
如图,已知:PA切⊙O于A,割线PBC交⊙O于B,C,PD⊥AB于D,延长PD交AO的延长线于E,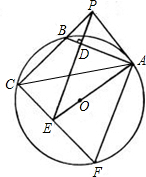 连接CE并延长,交⊙O于F,连接AF.
连接CE并延长,交⊙O于F,连接AF.
(1)求证:PD•PE=PB•PC;
(2)求证:PE∥AF;
(3)连接AC,若AE:AC=1: ,AB=2,求EF的长.
,AB=2,求EF的长.
(1)证明:∵PA切⊙O于点A,
∴AO⊥PA.
∵PD⊥AB,
∴ =cos∠APE=
=cos∠APE=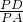 .
.
∴PA2=PD×PE…①
∵PBC是⊙O的割线,PA为⊙O切线,
∴PA2=PB×PC…②
联立①②,得PD•PE=PB•PC;
(2)证明:∵PD•PE=PB•PC(已证),
∴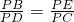 ,
,
∵∠BPD为公共角,
∴△BDP∽△EPC,
∴∠PBD=∠PEC,
∵四边形ABCF内接圆,
∴∠ABP=∠AFC,
∴∠AFC=∠PEC,
∴PE∥AP;
(3)解:∵AP是⊙O的切线,
∴∠PAB=∠PCA,
∵∠APB=∠CPA,
∴△PAB∽△PCA,
∴ =
=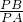 …①,
…①,
∵∠PAE=∠ADP=90°,
∴∠APD+∠PAD=90°,
∠APD+∠AEP=90°,
∴∠PAB=∠AEP=∠FAE,
∵∠ABP=∠F,
∴△AEF∽△APB,
∴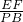 =
=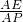 ,即
,即 =
=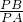 …②
…②
联立①②,有 =
= ,
,
∴EF=AE× =
= ×2=
×2= .
.
分析:(1)欲证PD•PE=PB•PC,在此题所给的已知条件中,∠APE的余弦值在△APD和△APE中,有两种表示方法,从而得出一个等积式,根据切割线定理,再得到一个等积式,从而借助于PA2得到PD•PE=PB•PC;
(2)可证△PBD∽△PEC,再根据相似三角形的性质和圆内接四边形的性质得到∠PEC=∠AFC,根据平行线的判定即可得出结论;
(3)分别证明△PAB∽△PCA,△AEF∽△APB,得出两个比例式,联立有 =
= ,再代值即可求出EF的长.
,再代值即可求出EF的长.
点评:此题考查了三角函数、切割线定理,以及相似的判定和性质,比较全面,有一定的难度.
∴AO⊥PA.
∵PD⊥AB,
∴
 =cos∠APE=
=cos∠APE=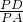 .
.∴PA2=PD×PE…①
∵PBC是⊙O的割线,PA为⊙O切线,
∴PA2=PB×PC…②
联立①②,得PD•PE=PB•PC;
(2)证明:∵PD•PE=PB•PC(已证),
∴
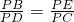 ,
,∵∠BPD为公共角,
∴△BDP∽△EPC,
∴∠PBD=∠PEC,
∵四边形ABCF内接圆,
∴∠ABP=∠AFC,
∴∠AFC=∠PEC,
∴PE∥AP;
(3)解:∵AP是⊙O的切线,
∴∠PAB=∠PCA,
∵∠APB=∠CPA,
∴△PAB∽△PCA,
∴
 =
=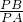 …①,
…①,∵∠PAE=∠ADP=90°,
∴∠APD+∠PAD=90°,
∠APD+∠AEP=90°,
∴∠PAB=∠AEP=∠FAE,
∵∠ABP=∠F,
∴△AEF∽△APB,
∴
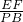 =
=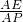 ,即
,即 =
=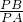 …②
…②联立①②,有
 =
= ,
,∴EF=AE×
 =
= ×2=
×2= .
.分析:(1)欲证PD•PE=PB•PC,在此题所给的已知条件中,∠APE的余弦值在△APD和△APE中,有两种表示方法,从而得出一个等积式,根据切割线定理,再得到一个等积式,从而借助于PA2得到PD•PE=PB•PC;
(2)可证△PBD∽△PEC,再根据相似三角形的性质和圆内接四边形的性质得到∠PEC=∠AFC,根据平行线的判定即可得出结论;
(3)分别证明△PAB∽△PCA,△AEF∽△APB,得出两个比例式,联立有
 =
= ,再代值即可求出EF的长.
,再代值即可求出EF的长.点评:此题考查了三角函数、切割线定理,以及相似的判定和性质,比较全面,有一定的难度.

练习册系列答案
相关题目
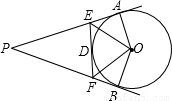
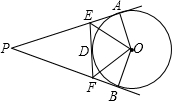 如图,已知:PA、PB、EF 分别切⊙O 于A、B、D,若PA=10cm,那么△PEF 周长是
如图,已知:PA、PB、EF 分别切⊙O 于A、B、D,若PA=10cm,那么△PEF 周长是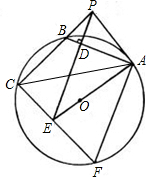 连接CE并延长,交⊙O于F,连接AF.
连接CE并延长,交⊙O于F,连接AF.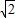 ,AB=2,求EF的长.
,AB=2,求EF的长.