题目内容
高致病性禽流感是比SARS病毒传染速度更快的传染病.
(1)某养殖场有8万只鸡,假设有1只鸡得了禽流感,如果不采取任何防治措施,那么,到第二天将新增病鸡10只,到第三天又将新增病鸡100只,以后每天新增病鸡数依此类推,请问:到第四天,共有多少只鸡得了禽流感病?到第几天,该养殖场所有鸡都会被感染?
(2)为防止禽流感蔓延,政府规定:离疫点3千米范围内为扑杀区,所有禽类全部扑杀;对扑杀区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如右上图,O为疫点,在疫点距公路最短2千米处有一 个提醒标志牌,问如有一辆汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区?
个提醒标志牌,问如有一辆汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区?
(1)某养殖场有8万只鸡,假设有1只鸡得了禽流感,如果不采取任何防治措施,那么,到第二天将新增病鸡10只,到第三天又将新增病鸡100只,以后每天新增病鸡数依此类推,请问:到第四天,共有多少只鸡得了禽流感病?到第几天,该养殖场所有鸡都会被感染?
(2)为防止禽流感蔓延,政府规定:离疫点3千米范围内为扑杀区,所有禽类全部扑杀;对扑杀区内的村庄、道路实行全封闭管理.现有一条笔直的公路AB通过禽流感病区,如右上图,O为疫点,在疫点距公路最短2千米处有一
 个提醒标志牌,问如有一辆汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区?
个提醒标志牌,问如有一辆汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区?分析:(1)根据规律得到第四天,共有1+10+100+1000=1111只鸡得了禽流感;第五天,共有1111+10000=11111只鸡得了禽流感,那么到了第六天将会有十多万只鸡会得禽流感,即可得到所有的鸡都会感染禽流感的时间;
(2)过O作直线AB的垂线,垂足为F,F即为提醒标志牌的位置,OF长度为2千米,连接OD,由扑杀半径为3千米得到OD为3千米,在直角三角形ODF中,根据勾股定理求出DF的长,即可求出汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区.
(2)过O作直线AB的垂线,垂足为F,F即为提醒标志牌的位置,OF长度为2千米,连接OD,由扑杀半径为3千米得到OD为3千米,在直角三角形ODF中,根据勾股定理求出DF的长,即可求出汽车朝疫区驶来,在距标志牌多远处就进入禽类扑杀区.
解答:解:(1)第四天,共有1+10+100+1000=1111只鸡得了禽流感;
第五天,共有1111+10000=11111只鸡得了禽流感,
那么到了第六天将会有十多万只鸡会得禽流感,而养殖场有8万只鸡,
所以到第六天,所有的鸡都会感染禽流感;
(2)如图,过O作OF⊥DE于F,连接OD,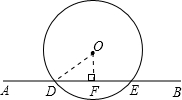
∴点F为提醒标志牌的位置,
∵OD=3千米,OF=2千米,
在Rt△ODF中,根据勾股定理得:DF2=OD2-OF2,
即DF=
=
(千米),
则汽车在距标志牌
千米就进入禽类扑杀区.
第五天,共有1111+10000=11111只鸡得了禽流感,
那么到了第六天将会有十多万只鸡会得禽流感,而养殖场有8万只鸡,
所以到第六天,所有的鸡都会感染禽流感;
(2)如图,过O作OF⊥DE于F,连接OD,

∴点F为提醒标志牌的位置,
∵OD=3千米,OF=2千米,
在Rt△ODF中,根据勾股定理得:DF2=OD2-OF2,
即DF=
| 32-22 |
| 5 |
则汽车在距标志牌
| 5 |
点评:本题考查了垂径定理,以及勾股定理,解答此类题常常利用圆的半径,弦的一半以及弦心距构造直角三角形,利用勾股定理来解决问题,在做第二问时,认真审清题意,作出相应的辅助线是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
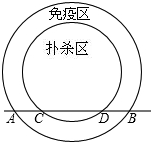 病区,如图,在扑杀区内公路CD长为4km.
病区,如图,在扑杀区内公路CD长为4km. 高致病性禽流感是比SARS病毒传染速度更快的传染病.
高致病性禽流感是比SARS病毒传染速度更快的传染病.
