题目内容
一元二次方程ax2+bx+c=0（a≠0）有两根x1，x2，则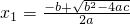
，
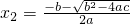，则x1+x2=________，x1x2=________．
请运用上面你发现的结论，解答问题：
已知x1，x2是方程x2-x-1=0的两根，不解方程求下列式子的值：
①x12+x22；
②
；
③（x1+1）（x2+1）．
-
分析：首先通过计算得出x1+x2和x1x2，从而发现规律，然后根据规律也就是根与系数的关系对下面的式子进行变形求解．
解答：由题意知：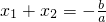
，
．
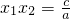根据结论有：x1+x2=1，x1x2=-1
则①x12+x22=（x1+x2）2-2x1x2=1-2×（-1）=3；
②=
=
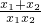=-1；
③（x1+1）（x2+1）=x1x2+x1+x2+1=-1+1+1=1．
点评：本题主要考查根与系数的关系，关键是找到规律，化简求解．
分析：首先通过计算得出x1+x2和x1x2，从而发现规律，然后根据规律也就是根与系数的关系对下面的式子进行变形求解．
解答：由题意知：
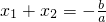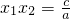，．根据结论有：x1+x2=1，x1x2=-1
则①x12+x22=（x1+x2）2-2x1x2=1-2×（-1）=3；
②
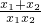===-1；③（x1+1）（x2+1）=x1x2+x1+x2+1=-1+1+1=1．
点评：本题主要考查根与系数的关系，关键是找到规律，化简求解．
练习册系列答案
相关题目
一元二次方程ax2+bx+c=0（a≠0，b2-4ac≥0）的两实根之和（ ）
| A、与c无关 | B、与b无关 | C、与a无关 | D、与a，b，c都有关 |
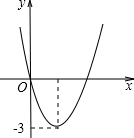（2012•泰安）二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）